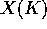 is not Zariski - dense in X. As noted in [
is not Zariski - dense in X. As noted in [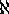 ], this implies
that if X is a variety which only dominates a variety of general type
then
], this implies
that if X is a variety which only dominates a variety of general type
then 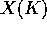 is still not dense in X.
is still not dense in X.



We work over fields of characteristic 0.
Let X be a variety of general type defined over a number field K. A well
known conjecture of S. Lang [L] states that the set of rational
points 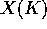 is not Zariski - dense in X. As noted in [
is not Zariski - dense in X. As noted in [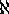 ], this implies
that if X is a variety which only dominates a variety of general type
then
], this implies
that if X is a variety which only dominates a variety of general type
then 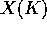 is still not dense in X.
is still not dense in X.
J. Harris proposed a way to quantify this situation [H1]: define the
Lang dimension of a variety to be the maximal dimension of a variety of
general type which it dominates. Harris conjectured in particular that if the
Lang dimension is 0 then for some number field 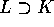 we have that
the set of L rational points
we have that
the set of L rational points 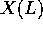 is dense in X. The full statement of
Harris's conjecture will be given below (Conjecture 2.3).
is dense in X. The full statement of
Harris's conjecture will be given below (Conjecture 2.3).
The purpose of this note is to provide a geometric context for Harris's conjecture, by showing the existence of a universal dominant map to a variety of general type, which we call the Lang map.