 |
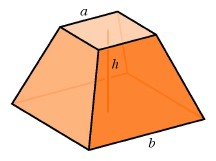
An incomplete pyramid
The rule for finding the volume of a pyramid was of great practical significance to the ancient Egyptians. They could have discovered it easily comparing the amount of sand needed to fill pyramid-shaped and prism-shaped boxes. After filling the pyramid three times with the sand from one prism, they could have realized that the formula for the pyramid is simply one-third times the formula for the prism. Much more difficult to discover by experiment is a formula for finding the volume of an incomplete pyramid, constructed up to a certain level, with the top still to come. How much additional material is necessary to complete the project? Finding such a rule was the most sophisticated discovery of anclent Egyptian geometry, and it leads to our final example of the ways algebraic and geometric patterns work in higher dimensions.
| |
An incomplete pyramid |
|
In order to obtain an intuitive feel and to acquire some important information at the same time, we consider the two-dimensional case of the same problem, the calculation of the area of an incomplete triangle, a trapezoid formed by cutting off the top of a triangle by a line parallel to its base. The key to finding a formula in this case is the principle of similarity. If two triangles are similar, then their bases and their heights are proportional.
We can extend the sides of the trapezoid to complete the triangle. This
large triangle is composed of the original trapezoid and a smaller
triangle, similar to the larger one. We do not know the height of either
triangle, but we know that the ratio of their heights is equal to the ratio
of their bases, and this ratio is the same as the ratio of the top and
bottom edges of the trapezoid.
| ||
The area of a trapezoid is the difference between the areas of two triangles. | ||
The area of a triangle is one-half the base multiplied by the height, If a denotes the base and x the height, then the area is ax/2. Analogously, if we have a pyramid of height x and square base of side length a, then the area of the base is a2 and the volume is xa2/3.
Letting x denote the height of the small triangle, the height of the
large triangle is
| (x + h)b 2 |
- | xa 2 |
= |
| |||||
| = |
| ||||||||
A famous algebraic identity states that
| |
The volume of an incomplete pyramid is the difference between the volumes of two pyramids. |
|
An analogous method reveals the formula for the volume of the incomplete
pyramid. We are given the height h of the incomplete pyramid and the side
lengths a and b of the top and the bottom squares. If the
height of the large pyramid is
| (x + h)b2 3 |
- | xa2 3 |
= |
| ||||||
| = |
| |||||||||
| = |
| |||||||||
The last step is an application of a standard algebraic identity, expressing the difference of two cubes in factored form:
This is the formula known to the ancient Egyptians and described by them in a papyrus dating back to 1800 B.C., using language considerably more complicated than the algebraic formulation given above. The formula represents a high point in the geometry of the ancient world.
What about the fourth dimension? In a purely formal way, the algebraic pattern suggests that if some four-dimensional artisan constructed a hyperpyramid with height x and a cubical base with edges of length a, then its four-dimensional volume would be xa3/4. The four-dimensional volume of an incomplete hyperpyramid would then be given by
| (x + h)b3 4 |
- | xa3 4 |
= |
| |||||
| = |
| ||||||||
| = |
| ||||||||
We can imagine that a four-dimensional artisan would be as pleased with the discovery of such a formula as the three-dimensional geometer who found the formula for the incomplete pyramid in ancient Egypt.
| Scaling and Growth Exponents
| ||
| Table of Contents | ||
| Diagonals of Cubes in Different Dimensions |