 |
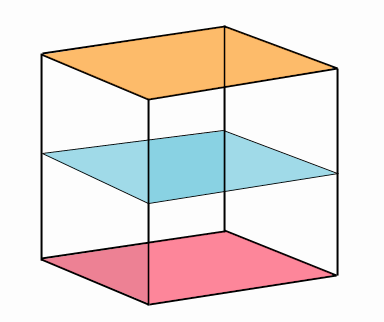
Slicing the cube square first.
When Abbott wrote Flatland, he was certainly aware of the work of Friedrich Froebel, the educational pioneer who invented the term kindergarten and who stressed the importance of presenting young children with geometric stimuli. By the 1880s, Froebel's ideas were beginning to influence preschool education in England and the United States, as they had in Prussia and other parts of Europe earlier in the nineteenth century.
One of Froebel's first "gifts" to inspire kindergarten children was a display of three basic three-dimensional forms, the sphere, the cylinder, and the cube, suspended by strings. As the objects rotated, children could observe them from different views and learn to appreciate their symmetries and structures.
The objects could be suspended in different ways from eyelets attached to their surfaces. Because of its symmetry, the sphere had only one eyelet, and no matter how it was suspended, it looked the same. The cylinder had three eyelets, one in the center of the top disc, one on the rim, and one halfway down on the side of the cylinder. The cube also had three eyelets, one in the center of a square face, one on the center of an edge, and one at a vertex.
If we suspend the objects from various points, we get different views and, more significantly, different sequences of horizontal slices. We can imagine what will happen if we gradually submerge the set of blocks in a pail of water. How will the shape of the slice formed at the water's surface change? The investigation of different slices of ordinary objects can give us a much better appreciation of their symmetries, as well as the ways their various parts fit together. Such observations will aid us in analyzing more complicated figures in ordinary space, and prepare for the later study of phenomena coming from higher dimensions.
When the sphere goes through the plane, the slicing sequence re-creates the visitation story in Flatland: a point, then a small circle, which grows to a large circle, which then shrinks down to a point and disappears. No matter how we suspend the sphere, the story is the same.
Submerging the cube gives more complicated and more interesting results. The three different ways of suspension lead to three very different slicing sequences. We see the least variable series of slices when the cube is suspended from an eyelet in the center of a square face. As the water level rises, all slices are squares, all the same size. If A Square were floating on the surface of the water, he would report that suddenly out of nowhere there had appeared in front of him a square like himself, which remained there for a while, and then abruptly disappeared. He would describe the cube as "a square for a while," mistakenly interpreting one of the dimensions of space as a dimension of time.
| ||
Slicing the cube square first. |
How can A Square begin to appreciate what actually happened? In the story, A Square is prepared for understanding such a visitation by a vision of Lineland, a world of only one dimension. The King of Lineland is a long segment, who cannot "see" anyone beyond those two subjects immediately adjacent to him. When A Square visits this realm, edge first, the King considers him to be "a segment for a while."
What would we see if we were visited by a four-dimensional hypercube? If it came through our space "cube first," we would see "a cube for a while." Our position would be analogous to that of A Square trying to come to terms with a visit of a three-dimensional cube, or the King of Lineland trying to comprehend the passage through his land of A Square.
As it happens, slicing sequences reveal some of an object's important properties. For one thing, we can figure out how many corners or vertices the analogue of a cube has in each dimension. The King knows that as a segment he has 2 vertices, which we might think of as bright points. As he watches the "segment for a while," he sees two bright points at the first instant and two more at the end, so he knows the square has 4 vertices. A Square could appreciate that a cube has 8 corners even though he cannot see a cube all at once in his flat world. A "square for a while" has 4 bright vertices at the first instant and 4 more at the final moment, for a total of 8. Similarly, a hypercube, thought of as "a cube for a while," would have 8 bright vertices at the start and 8 more at the end, for a total of 16 vertices. Even though we can never hope to "see" a hypercube all at once in the same way that we see a cube, we can have confidence that if we ever do see such an object, it will have 16 vertices. If we ever see anything with more vertices or fewer, we will know that it is not a hypercube.
In Flatland, we are encouraged not to stop at the second dimension or the third or even the fourth. If we continue the analogy, we can imagine that a five-dimensional cube passing through a four-dimensional "still pond" will appear as "a hypercube for a while," with 32 vertices. Each time we go up a dimension, the number of vertices is multiplied by two. Thus it is that the number of vertices in a square is two times two, or two squared, and the number of vertices of a three-dimensional cube is two cubed. The pattern is clear: in a space of any given number of dimensions, the number of vertices of a cube in that dimension is a power of two, with one factor of two for each dimension. (We may symbolize this by saying that the number of vertices of a cube in n dimensions is 2n.)
Note that we have not raised the question about whether or not a hypercube actually exists as a physical object. Mathematicians are interested in describing properties of geometric objects whether or not they correspond to any objects that exist in any physical sense. As a mathematical object, a hypercube is an abstraction, but so is a cube or a square. No one has ever seen a perfect square or cube, but nonetheless we can grasp the idea of these shapes. We can also grasp the idea of the hypercube.
| Slicing from Other Directions | ||
| Table of Contents | ||
| Introduction |