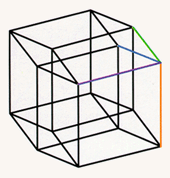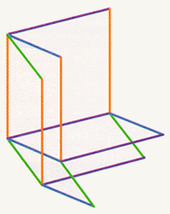
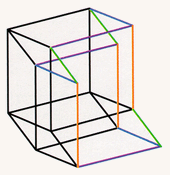
Using computer graphics, we can analyze the shadows of a three-dimensional building even before it is constructed. And we can do more. We can investigate the shadows of objects that never could be built with our three-dimensional materials, for example the four-dimensional hypercube. We can draw a hypercube on the page of a book the same way we drew the two- and three-dimensional cubes, by drawing the images of the edges coming out of one corner and then drawing a collection of parallel edges to complete the figure. Two edges emanating from a point determine the image of a square, and three edges determine the image of a cube. Four edges emanating from a point will determine the image of a four-dimensional cube. First taking two edges at a time, we complete six parallelograms; then taking three edges at a time, we complete the images of four different cubes. Drawing the remaining four edges will complete the figure.

	Left: Starting from four edges, six squares are drawn at the vertex of the hypercube. Center: Adding the rest of the four cubes at the vertex of the hypercube. Right: The complete hypercube, containing four sets of parallel edges.

We can generalize this process to even higher dimensions since each dimension has its analogue of the cube. If we draw five edges from a corner, we can complete the image of a five-dimensional cube, or five-cube. There is nothing to stop us from drawing shadows of hypercubes of any number of dimensions on a two-dimensional paper or a two-dimensional computer screen.

We can't construct a hypercube in four-dimensional space and draw its actual shadow, but we don't have to. We know that if such a cube existed and if it cast a shadow on a wall, then we would have four groups of eight parallel edges. If the initial set of four edges changed slightly, then the whole figure would follow along, and by recording a succession of slightly changed images, we would obtain an animated cartoon of the transforming object. Naturally this process would be tedious to do by hand. Already in the last century mathematicians and draftspersons sketched individual shadows of this type, but it took the development of modern graphics computers to produce animated films of rotating hypercubes. The first such films were made by A. Michael Noll and his associates at Bell Laboratories in the 1960s. The most complete version, The Hypercube: Projections and Slicing, was produced by Charles Strauss and the author at Brown University in 1978 as part of an invited presentation at the International Congress of Mathematicians in Helsinki.

			Three-Dimensional Shadows of the Hypercube
			Table of Contents
			Drawing Cubes and Hypercubes