 |
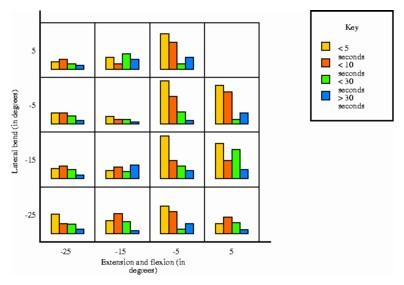
In this graphing of goniometer readings the height of the bars indicates the amount of time spent in bending and flexing during the performance of a task.
To study the range of possible positions, researchers attach to a worker a device called a goniometer, which records back position by keeping track of three angles. Two angles give the position of the spine, in coordinates roughly like latitude and longitude. The third coordinate measures the angle of the sideways twist of the shoulders relative to the pelvis. These three numbers describe a configuration that is the position of the device (and its wearer) at any instant during the course of the job. If we display these coordinates on a three-dimensional grid, then any single configuration corresponds to a point on this grid. We call this collection of points in three-space the configuration space for this particular example. As a worker moves from one position to another, the corresponding point moves from one location to another in the configuration space. As a worker moves through a whole series of tasks, we obtain a series of points tracing out a path in the configuration space describing the physical demands of the job.
The record of such a path in a three-dimensional space does not describe the actions of the worker completely. There is no information here that tells whether a person has walked to another location, or climbed a ladder, while bending and twisting. Only the bending and twisting are recorded since those are the significant variables in assessing the condition of the lower back.
Each job has its own dimensionality, depending on the number of different directions of bending and twisting the job involves; the more directions, the higher the dimension of the configuration space where we keep track of the possible positions a worker assumes. A park attendant collecting pieces of paper bends over many times, always in the same direction, and the goniometer registers the changes in this one and only angle. It would be possible to describe the bendings that take place over an entire day on a sort of seismograph, producing a strip of paper showing the angle reading at each time. One could then easily determine how often the park attendant bent over past a certain angle, and for how long. In terms of the goniometer, the park attendant has a one-dimensional job.
A secretary may bend from side to side as well as bend forward. His positions can then be specified by two coordinates. Since there is no twisting, the third coordinate angle is always zero, and the state of his lower back at any particular time can be indicated by a point on a two-dimensional grid. As he goes through the motions of his job, the recording point could trace out a path on a two-dimensional computer screen, an ``orbit'' in the configuration space. Note that in this example there is no time axis. If we wanted to know at what time the secretary assumed a given position, we would have to label the corresponding point on the two-dimensional record sheet.
| ||
In this graphing of goniometer readings the height of the bars indicates the amount of time spent in bending and flexing during the performance of a task. |
Researchers at the University of Vermont analyze such orbits by dividing the grid up into cells. By noting the number of times an orbit curve enters a particular cell during a workday, they can measure the complexity and demands of the job. They can then determine which kinds of orbits are suitable for workers with different injuries.
For a job that requires twisting as well as two different kinds of bending, each goniometer reading has three coordinates, and the orbit curve will lie in a three-dimensional space. Once again the technique is to divide the configuration space into cells or ``bins'' and to see how many times the orbit curve enters different bins in the space. As we have seen in previous chapters, analyzing a geometric object in three-space often involves projecting it into two-dimensional planes, and that is what occurs here as well.
Not all the variables in lower back research can be described in a three-dimensional configuration space. The rehabilitation therapist might wish to consider additional variables affecting the lower back, like the weight of load to be lifted or the temperature of the environment, so the appropriate configuration space might have more than three dimensions. To analyze a collection of points in a configuration space of four or five dimensions, researchers make use of the geometric techniques similar to those that we have developed for analyzing fundamental objects like hypercubes. Such higher-dimensional structures can form the framework for the understanding and interpretation of data from many different fields.
| Dimensionality and Dance | ||
| Table of Contents | ||
| Introduction |