 |
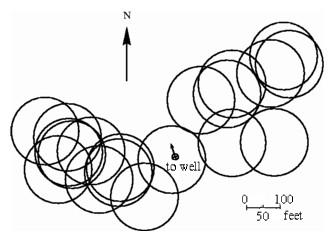
Overlapping circle patterns show the location of campsites and the areas covered by hunting parties near the Mulyangiril well in Western Australia.
Lower-dimensional configurations of circles arise in fields far from physics and mathematics, and a geometric understanding of dimensions can help there as well. Professor Richard Gould in the Anthropology Department at Brown University found a specific use for the configuration space of circles in the plane while organizing data about hunter-gatherers in the Australian bush. A colony of hunter-gatherers can maintain a fixed location as long as its hunters can find a supply of game in all directions. From the central campfire, hunting parties spread over a large area, which can be considered as a disc with a given radius. If large predators threaten, hunters will return each night to a secure camp and the size of the disc will be relatively small. In the absence of major threats, they can stay away for one or more nights before returning to camp, and the area of the disc centered at the campsite will be larger. Ultimately the campsite will be moved. Gould wanted to know how far a colony would move, and what the pattern of movement is over time.
To keep track of a number of circles, Gould recorded each one with three numbers, using latitude and longitude to give the position of the campfire and a third number to give the radius of the disc. The space of discs is then three-dimensional, and the movement of the colony determines a sequence of points in this space, a ``polygon in the space of circles.'' To find the total area of the campsites over time requires knowledge of the ways the discs overlap, and here the three-dimensional recording system has an additional advantage--for each pair of sites, Gould could compute a number telling whether or not they overlap, and in particular whether or not one site is completely contained in another.
| ||
Overlapping circle patterns show the location of campsites and the areas covered by hunting parties near the Mulyangiril well in Western Australia. |
As it happens, the mathematics of this problem has a curious history. The space of circles was studied as a mathematical subject in the last century by the French mathematician Edmond Laguerre. He thought of the triple representing a given disc as a point in ordinary three-dimensional space, and the condition for two discs to be intersecting, or for one to contain the other, was given by attaching a ``distance'' to a pair of points in space. But instead of using the ordinary Pythagorean theorem to represent the distance in terms of a sum of squares, Laguerre's distance involved the difference of squares. It was precisely this sort of generalized distance that turned out to be significant in the geometry of relativity. We can develop this notion further by investigating a less realistic configuration space, the space of spotlights on a stage.
| The Dimensionality of Stage Lighting | ||
| Table of Contents | ||
| Orbits of Dynamical Systems |