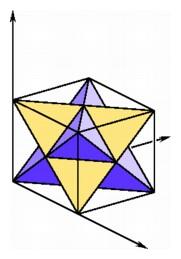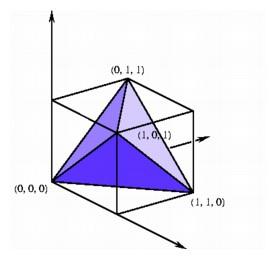
We have already seen how the vertices of an n-cube can be represented in n-space using only zeros and ones as coordinates. It is often somewhat harder to give a simple coordinate description of an n-simplex in n-space. It is not always a difficult task--there is a perfectly good choice for the vertices of a three-simplex in three-space obtainable by taking four of the eight vertices of a three-cube, for example (0, 0, 0), (1, 1, 0), (0, 1, 1), and (1, 0, 1). We know that this tetrahedron is regular because the distance between any two of its vertices is 2^1/2. The remaining four vertices of the cube, (1, 0, 0), (0, 1, 0), (0, 0, 1), and (1, 1, 1), also determine a regular tetrahedron. These two overlapping tetrahedra fit together to form a figure called the stella octangula, and their intersection is the dual octahedron contained in the cube.

	The regular tetrahedron in the unit cube (left); the stella octangula formed by two intersecting tetrahedra in the unit cube (right).

However, if we want to find coordinates for the two-simplex in the plane, the situation is more complicated. If we choose the two coordinate pairs to be (0, 0) and (1, 0), then the third coordinate will be either (1/2, 3^1/2/2), or (1/2, -3^1/2/2), and so we obtain fractions and irrational numbers as coordinates. There is no way to avoid using irrational numbers in the coordinates of an equilateral triangle as long as we stay in the plane. If, however, we are willing to go to three-space, then we can find a perfectly simple collection of points forming the vertices of a regular two-simplex, for example three of the vertices of the second regular tetrahedron given above, (1, 0, 0), (0, 1, 0), and (0, 0, 1).

	Irrational coordinates for the regular two-simplex in the plane (left); rational coordinates for the regular two-simplex in three-space (right).

Not only do these points with one coordinate 1 and all the rest 0 give a satisfactory solution to the problem of representing a two-simplex with simple coordinates, they also provide a method for finding coordinates of a simplex of any dimension. To find a coordinate representation for the n + 1 vertices of an n-simplex, we can take the points at unit distance along the coordinate axes in (n + 1)-space. This is a natural approach from the point of view of slicing since the configuration of the vertices near each corner of an (n + 1)-cube is an n-simplex. For example, when we slice perpendicular to the long diagonal of a hypercube from (0, 0, 0, 0) to (1, 1, 1, 1), one of the slicing hyperplanes contains the four vertices (1, 0, 0, 0), (0, 1, 0, 0), (0, 0, 1, 0), and (0, 0, 0, 1). Since the distance between any two of these vertices is 2^1/2, they are the vertices of a regular three-simplex.

			Coordinates for Hypercube Slices
			Table of Contents
			Lengths and the Generalized Pythagorean Theorem