 |
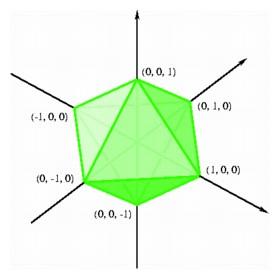
Coordinates for the octahedron.
We have just obtained a set of coordinates for the vertices of a regular three-dimensional octahedron thought of as the middle slice of a hypercube in four-dimensional space. It is also easy to give a three-dimensional coordinate description for the octahedron by taking advantage of the fact that the octahedron is the dual of the cube: the vertices of a regular octahedron can be obtained as the centers of the six square faces of a cube. If we choose coordinates for the vertices of the cube, we can figure out the coordinates of the centers of square faces and obtain the coordinates for the vertices of the octahedron. In the previous paragraph, we studied a cube with vertices having all coordinates 0 or 1, but in considering the dual, it turns out to be more convenient to start with a cube centered at the origin having all coordinates -1 or 1.
| ||
Coordinates for the octahedron. |
What about the other regular polyhedra in three-space? We can exploit the symmetry of the icosahedron to come up with some fairly satisfactory coordinates, involving just one irrational number. And a very important number it is. We start by observing that for every edge of the icosahedron there is a parallel edge on the opposite side. We may situate the icosahedron in the cubical box so that all 12 vertices are on the boundary of the box and in fact so that the intersection with the boundary of the box consists of six edges parallel to the coordinate axes. As provisional coordinates for these segments, we may choose (±1, 0, ±t), (0, ±t, ±1), and (±t, ±1, 0), where t is a number to be chosen later. In general, the polyhedron with these 12 vertices will have edges of two lengths: 2t for the edges on the boundary of the box and (1 + t2 + (1-t)2)1/2 for the other edges. In order for the icosahedron to be regular, the lengths of all these segments should be equal. This condition leads to the algebraic equation t2 + t - 1 = 0, with positive solution t = (-1 + 51/2)/2. This important number appears in all sorts of contexts involving the concepts of growth and form. It is called the golden ratio, and it expresses the ratio of a side of a regular pentagon to one of its diagonals. We should not be surprised to see it appear in conjunction with the regular icosahedron since the vertex configuration of each corner of this object is a regular pentagon.
| ||
Choosing different values of t opens up the octahedron (t = .1) by inserting isosceles triangles along its edges (left). For a special value (t ~ .618), the triangles are all equilateral and we have coordinates for the regular icosahedron (right). |
It is possible to get a set of coordinates of the regular dodecahedron by taking the centers of the faces of the icosahedron given above, but we can find the coordinates more directly by exploiting another relationship with the cube. We start with a particular diagonal of a pentagonal face of the dodecahedron, then choose diagonals in the adjacent faces so that the three diagonals meeting at a vertex are mutually perpendicular and all of the same length. If we continue this procedure, we obtain 12 diagonals fitting together to form the edges of a cube inscribed in the dodecahedron, with one edge for each of the 12 faces of the dodecahedron. By starting with different diagonals of the original pentagon, we end up with five different cubes; in this collection of cubes, each of the 60 diagonals of the dodecahedron is used exactly once. By choosing the 8 vertices of the cube first, we may use the symmetry of this figure to find coordinates for the other 12 vertices of the dodecahedron. If the vertices of the cube are (±1, ±1, ±1), then the others are of the form (±t, 0, ±1/t), (0, ±1/t, ±t), and (±1/t, ±t, 0), where t is the same number appearing in the coordinates for the icosahedron.
| Coordinates for Regular Polytopes | ||
| Table of Contents | ||
| Coordinates for Hypercube Slices |