 |
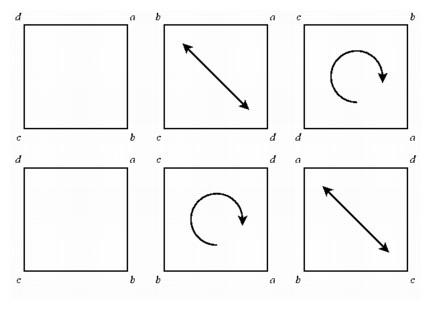
Reflecting across a diagonal then rotating a quarter turn (top) gives a different effect from rotating a quarter turn then reflecting (bottom).
For the realists, especially the followers of the influential German philosopher Immanuel Kant, the essence of geometry was that it described experience. The suggestion that some new system of statements deserved to be called geometry was a threat. Yet the followers of Kant did not object when formulas in algebra no longer seemed to describe reality. Certainly a great many of thc most familiar algebraic relationships originated from real problems, some of them geometric and some from economics and physical science. Parabolas were familiar as conic sections and as the paths of projectiles, and the simple formula for a parabola could easily be graphed using the techniques of analytic geometry. Volume formulas suggested cubic equations, and they were also easy to graph and analyze. But it was not much harder to use the same techniques to analyze polynomials of degree four or five or higher. Few objected that this was not algebra, even though it no longer had a convenient geometric interpretation.
However, there was some resistance to algebraic innovation the first time someone suggested an algebraic operation that was not commutative. By this stage, mathematicians had written down axiom systems describing the ordinary algebra of real numbers. Among the rules describing addition and multiplication were two stating that the order of adding or multiplying was not important: the sum of a and b was the same as the sum of b and a, and the same was true for the product. Later, mathematicians began to realize that laws for combining elements in other sorts of systems satisfied most of the axioms of ordinary algebra, and so these systems behaved in large measure like numbers. An important example is the collection of symmetries of a square. We can rotate a square by one-quarter turn in a counterclockwise direction to move all four vertices. Rotating the square again results in a half turn and rotating once again yields a three-quarter turn. It does not matter in which order we make one turn after another. The rotational symmetries of the square form a commutative system.
But the collection of all symmetries of the square is not a commutative system. We can reflect a square across its diagonal, keeping two vertices fixed and interchanging the other two, or reflect about a horizontal or a vertical line through the center, moving all four vertices. When we combine such reflections with rotations, the order in which we apply them makes a difference. If we reflect across a diagonal and then rotate by a quarter turn, the effect is the same as a vertical reflection. On the other hand, if we first rotate by a quarter turn and then reflect across the diagonal, the effect is the same as a horizontal reflection. But although the collection of symmetries is not commutative, it is algebra, albeit noncommutative algebra. It satisfies many of the axioms for combining elements that characterize ordinary arithmetic but not all. Another accepted noncommutative system was the algebra of quaternions mentioned at the end of the last chapter. If it was relatively easy for people to accept noncommutative algebra, why was it so difficult for them to accept an alternate geometry, one that satisfied some but not all of the axioms of Euclid?
| ||
Reflecting across a diagonal then rotating a quarter turn (top) gives a different effect from rotating a quarter turn then reflecting (bottom). |
One difference was that many mathematicians did not really believe that the axioms of geometry were independent. They recognized that the commutative property of algebra could not be proved from the other axioms, since in fact they had in front of them an example of a consistent system that satisfied all other properties except commutativity. But in geometry many thought that it was just a matter of time until someone was able to prove the validity of the fifth axiom from the first four axioms. It was quite a surprise when just the opposite happened--mathematicians formulated systems that looked like geometry in that they satisfied the first four axioms, but they failed to satisfy the fifth. No one had suspected that there could be a geometry having triangles whose angles summed to greater than or less than 180 degrees, and then these geometries appeared.
| The Development of Non-Euclidean Geometry | ||
| Table of Contents | ||
| The Axioms of Euclidean Plane Geometry |