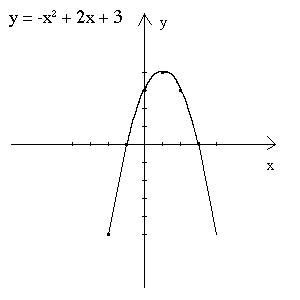
Step 3: Find the functions zeros by solving f(x) = 0.
f(x) = -x2 + 2x + 3
(-x + 3)(x+1) = 0
x = 3, -1.
Step 4: Find the critical points of the function by solving f'(x) = 0. Determine over which intervals the function is increasing or decreasing.
f'(x) = -2x +2 = 0
x = 1
f(x) is increasing over x = -infinity to 1 since f'(x) is positive there, and is decreasing over x = 1 to infinity since f'(x) is negative there.
Step 5: Find the inflection points of the function by solving f''(x) = 0. Determine over which intervals the function is concave up or down.
f''(x) = -2 so there are no inflection points.
Step 6: Calculate some y values of the function at one or two convenient x values. Proceed to draw the graph using information you have gathered.