Much of my discussion for chapter five (last week) focused on polyhedral duality in three and four dimensions. One of the main points was how duality changes context when it is considered in different dimensions: in three, duals are created by connec ting centers of 2D faces (squares in cube), while in four dimensions a dual is usually created by connecting centers of 3D cells (cubes in hypercube). I want to continue discussing duality in both dimensions here.
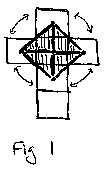
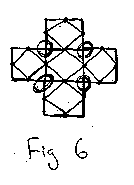
It can be difficult to get a good look at what is really going on when dealing with polytopes in three and four dimensions. An interesting strategy I stumbled upon is one that deals with examining duality by looking at the figures fold outs. I will start with a cube because of its level of intuitive quality. A cube fold out will have six squares aligned in the cross pattern. The dual to the cube will have a vertex at the center of each face, so we mark those with points. When we connect the cente rs of the squares to create the dual (just the five squares first), we get four right triangles connected in the plane sharing a common vertex.

This is very interesting. We know that the dual to the cube is the octahedron, which is i) eight equilateral triangles, and ii) two "diamond" (note: diamond and square are same thing in 2 space, and in this case diamond is more appropriate) based pyra mids sharing the same base diamond. So we can look at our four right triangles as i) half of the octahedron, the triangles of which will become equilateral when the squares are folded into a cube, or ii) a perspective view looking into the bottom half of an octahedron. When we add the last square with its centered vertex, four more triangles will be created (which are difficult to represent in the plane) by connecting to the four outer squares (just like the inside square did).
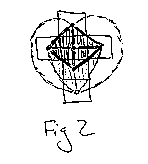
We can now do this for other three dimensional polyhedra, but I'd rather move directly to the hypercube instead (haven't checked out the other 3D polyhedra yet, but would assume similar results would be achieved). The folded out hypercube will have 8 cubes aligned in a very similar cross pattern with one internal cube that is "opposite" the last external cube. The dual to the hypercube will have a vertex at the center of each cell in the hypercube, so we mark those points. When we connect the cent ers of the cubes to create the dual (just the seven cells first), we get eight right tetrahedra sharing the same vertex, which is the center point of the "inside" cube.
We know from experience (and from "Beyond the Third Dimension") that the dual to the hypercube is the 16-cell, which is i) a composition of 16 regular tetrahedrons. But we know now, from both analogy and process, that the 16-cell is also ii) two octah edrons sharing the same "base surface" (base surface being the outer crust / shell / armor of the octahedron, analogous to the "base diamond" before, which was the outer edges of the "diamond based pyramid" base diamond). So we can look at our 8 right te trahedra as i) half of the 16-cell, the tetrahedra of which will become regular when the cubes are folded into a hypercube, or ii) a skewed perspective view looking into the bottom half of a 16-cell. When we add the last cube with its centered vertex, 8 more tetrahedra will be created by connecting to the eight triangles on the outside of the "inner octahedron".
In three space another type of polyhedral duality exists, creating irregular polyhedra (polyhedra composed of more than one type of regular two dimensional polygon) rather than regular ones.
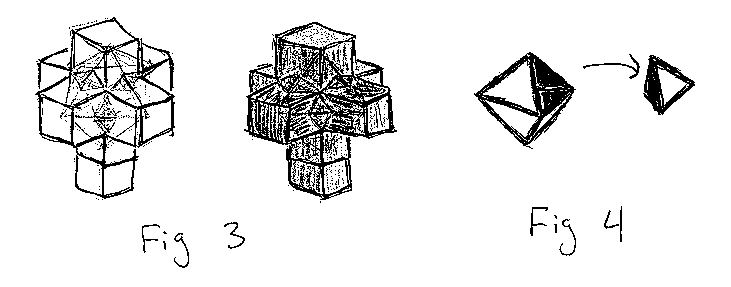
Note that another way of getting the same result, using a technique we've already used before, is unfolding the cube and looking at the "raw material" of our new irregular polyhedra. Each square has its dual, and each triangle has been separated and lies flat in the plane like a square (marked by the blue circles). Notice how the center of these "separated areas" are the corners of the cube. When the squares are folded up, any line of the inner diamond will act as the base for the triangles in our irregular polyhedra (the other lines of the triangles created out of the other diamonds). This will all come back when we check out 4D polytopes.
A table will hopefully be sufficient for the rest of the three dimensional polytopes:
Faces (become) ||||| Corners (become) |||| Product:
Tetrahedron: 4 faces -> 4 triangles |||| 4 corners -> 4 triangles |||| Octahedron
Cube: 6 faces -> 6 diamonds |||| 8 corners -> 8 triangles |||| 14 sided solid
Octagon: 8 faces -> 8 triangles |||| 6 corners -> 6 diamonds |||| 14 sided similar solid as above
Dodecahedron: 12 faces -> 12 pentagons |||| 20 corners -> 20 triangles |||| 32 sided solid
Icosohedron: 20 faces -> 20 triangles |||| 12 corners -> 12 pentagons |||| 32 sided similar solid to above
Now a few questions are raised. i) what is the relationship of the "similar solids"? ii) what happens if you connect the centers of the faces of the new irregular polyhedra? More duality right?
In four space more types of polyhedral duality exist, creating analogous irregular polytopes. These type of dualities involve connecting the center of the 2D faces and 1D edges of 4D polytopes rather than centers of the 3D cells. Once again, our original concept of duality, in this case three dimensional duality, appears in these new duality concepts. My work has only just begun, so I've only examined the new type of duality that is created by connecting the centers of the "faces" (2D obj ects) of a 4D polytope. I will begin with the hypercube. Because I can't just draw the hypercube, I start with the unfolded hypercube to get a look at the "raw materials" just like we did when we unfolded the cube. Working by analogy, as well as by act ually connecting the points, we see that each cell (cube) is transformed into its dual octahedron (the analog of the diamond).
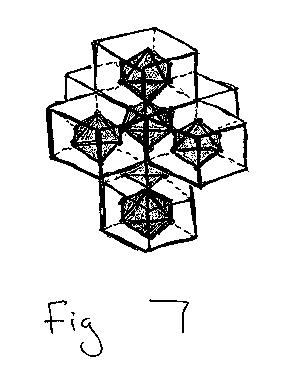
So we know we have 8 octahedra, six surrounding an inner one with an extra outer one at the bottom. Just as we had "spaces that aren't really spaces" before when we unfolded the cube, here we have volumes that are not really volumes. These volumes oc cur at the corners of the inner cube where, just as the third edge from the unfolded cube's vertex was split in two in our 3D example, our fourth edge at the hypercube vertex is seen in this fold out split three ways. More analogy, just as the spaces be fore became the triangles of our 3D irregular when we folded up our fold out, here our volumes will become some type of cell of our 4D irregular when we fold it up. The question is what type of cell will the fold up create? Notice that each corner of th e inner cube of the foldout is associated with one triangular face of its octahedron. These triangular faces will act as the "base surfaces" of our 3D cells when we fold the cubes into 4D, connecting the separated edges / points, just as the lines of the inner diamond in part A acted as the bases to what became the triangular faces of our 3D irregular polyhedron. So by analogy and observation we know that we will have (for one corner of the inner cube), a triangle base, each edge of which will be a part of a triangle created by the "trisected hypercube edge", giving four triangles aligned exactly as they are in an octahedron. In fact, when the cubes are folded up these "volumes that are not really volumes" become octahedra. Noting that 8 of these will be formed from the corners of the inner cube, 8 more from the corners of the outer cube, giving a total of 24 identical octahedra (we already had 8 from the original cube duals), which is commonly know as the 24-cell! As a check, the volume of an octahe dron (for a cube edge length of 2x) is 8x^3/3, which is 1/3 total volume of the cube. So 24 octahedra (total volume 64x^3) equals total volume of 8 cubes.
An easy way to come to this conclusion theoretically rather than through sketches, now that we have already "proved" it by looking at the actual raw materials, is take the two rules we used for creating our three dimensional irregular polyhedra: i) fa ces (or cells in this case) become their duals, and ii) the corners become whatever you get when you "shave" half way to the other one. So now it is all made very simple: the 8 cells become 8 octahedra, and the 16 vertices of hypercube become 16 octahed ra (p. 49 B3D), giving a total of 24 octahedra.
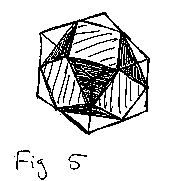
I've only just begun to look at 4D duality created by connecting the midpoint of edges (32 of them in the case of the hypercube). Using the same process as above, imagine the unfolded hypercube, each of the 8 cubes already "shaved" into the irregular polyhedra as described in part A before (figure5), folding together. Each virtex would become a tetrahedron (so 16 of them), and the final 4D irregular polytope would consist of these 16 tetrahedra and the oridinal 8 irregular polyhedra. More later poss ibly