Mathematics

The Mathematics of Symmetry

Everyone has some idea of what symmetry means. We can recognize symmetry in paper snowflakes, in the kitchen tiles, and even in our own bodies. We are attracted to it and fascinated by it. Yet, these vague impressions and definitions will only take us so far. In order to better understand symmetry and apply its concepts to science, mathematicians have developed a formalism for symmetry. This formalism is called group theory - the mathematical language of symmetry.

The Group: The Formal Definition

First and foremost, a group is a set of elements. A set is a collection, and its elements are whatever comprise the collection. Sets appear everywhere in math and are usually denoted like this:

S = {a, b, c}

S is the name of the set, and a, b, and c are its elements. The order, or number of elements, of this particular set is three. A set's order may or may not be finite - we will examine some infinite sets later on.

In order for a set to be classified as a group, it must have a law of composition (also known as the law of "multiplication"). This simply means that any two elements of the set can be combined in some way. For example, since a and b are elements of S, the compositions of those two elements are denoted ab and ba. Remember that this is merely the notation used for the law of composition and does not necessarily imply actual multiplication. In addition to the law of composition, a set must satisfy four other conditions to be classified as a group.

Closure: For all elements a, b of set G, ab, ba must also be elements of set G.
Associativity: For all elements a, b, c of set G, a(bc) = (ab)c.
Existence of Identity: G contains an element e called an identity element, such that for every element a of G, ae = ea = a.
Existence of Inverses: For every element a of G, there is an element of G denoted a^-
1, such that aa^-1 = a^-1a = e.

In some cases, a group will also have the property that ab = ba. Such a group is called Abelian. A diagram of a group, called a group table, reveals the structure of the group. It is a statement of the results of all possible compositions of pairs of elements.

Example of a group table

What does this have to do with symmetry?

In order to answer this question, we must remember that essentially, symmetry is immunity to change. You take an object, do something to it (rotate it, reflect it, etc.), and it remains the same. Or at least it looks the same. The act (the rotation, reflection, etc.) is a transformation. Groups consist of these transformations. We will consider several groups of different orders to demonstrate this.

Order 1
Since every group must contain the identity element e, there is only one abstract group of order 1, denoted C₁. A realization of this group might be the number 1, with multiplication as its composition. Or the number 0, with the composition of addition. Or 0 degrees, with rotation about an axis as its composition. All of these essentially leave an object unchanged.

Order 2
There is only one abstract group of order 2, denoted C₂, and it consists of the identity element e and one other element a. One example of a C₂ group could be {1, -1}, with composition of multiplication. A geometric realization could be {0 degrees, 180 degrees}, with composition of consecutive rotation. The axis of rotation is often referred to as a symmetry axis. Yet another geometric realization could consist of the identity transformation (the transformation of doing nothing) and the transformation of mirror reflection, under the composition of consecutive reflection. Note that the reflection and rotation are realizations of the same group - both describe the same structure. This is an example of isomorphism.

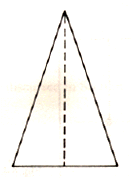
Example of C₂ symmetry

Order 3
C₃ is the only abstract group of this order, consisting of e, a, and b. It, too, has a rotational realization: {0 degrees, 120 degrees, and 240 degrees} under consecutive rotation. An example of third order symmetry might be an equilateral triangle.

Order 4
There are two different types of groups of order 4. The first, C₄, is similar to the prior groups we have discussed. One possible realization is {1, i, -1, -i} under multiplication, as well as the usual {0 degrees, 90 degrees, 180 degrees, 270 degrees} with consecutive rotation as the composition. The second, denoted D₂, is slightly more complicated. Imagine a pair of perpendicular, intersecting mirrors A and B with their line of intersection C. The group consists of: the identity transformation, a reflection through mirror A, a reflection through mirror B, and a rotation of 180 degrees about C. You might also note that a reflection through A, followed by a reflection through B, is the same as a 180 degree rotation; a reflection through A, followed by a 180 degree rotation, is the same as a reflection through B; a 180 rotation, followed by a reflection through B, is the same as a reflection through A; etc. (Remember the property of closure!) The D₂ group is an example of the general dihedral group D_n. We can be assured that C₄ and D₂ are two different groups because each has a distinct group table.

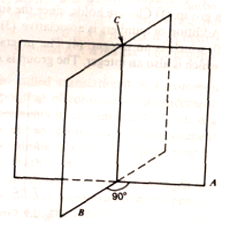
A realization of D₂

These are just a few examples of groups. All groups of order 5 or less are Abelian, which means it doesn't matter in what order you perform the transformations. Once you add more elements, things become more complicated, though generally groups of higher order are considered "more symmetrical." (Still, these were examples of finite-order groups. For a few examples of infinite-order groups click here.) One important thing to note is that each group could have several different realizations, and that these realizations might consist of numbers, matrices, rotations, or other geometric transformations. This allows mathematicians and scientists to express geometric properties in quantitative terms.

Symmetry Groups

A symmetry group is the complete set of an object's symmetries. For example, say we are trying to find the symmetry group of a square. There is rotational C₄ symmetry about the axis through the center of the square, reflections through each of the two planes containing the axis and a diagonal, and reflections through each of the two planes containing the axis and a parallel to the sides, the order 8 group D₄. Some of these symmetries could be isomorphic or subgroups of one another

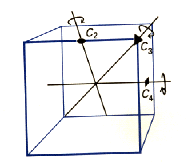
Symmetry axes of a Cube

Further Discussion

We have merely touched on the basics of the mathematical language of symmetry, for there are entire libraries devoted to group theory, symmetry applications, and different types of groups. One interesting field of study might be wallpaper groups, the study of symmetry in two-dimensional patterns. Often, these patterns' symmetry comes from repetition, or a tesselation. Symmetry in two-dimensional strips also has its own name, frieze groups. Three-dimensional patterns are often called lattices, prompting another field of study called lattice groups or space groups. And of course, symmetry can also be found in higher dimensions.

Sources