Inverse Relations of Complex Power Functions
Just as in the case of functions of a real variable, we can rotate the
graph of a complex function to exhibit the graph of its inverse
relation. In the case of the squaring function, this leads to a graph
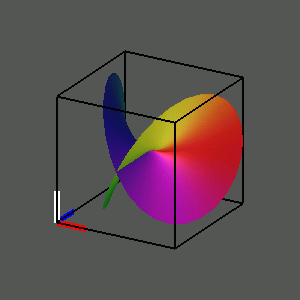
of the square root relation z = w^1/2, a complicated surface in
three-space that appears to intersect itself. As the figure rotates
in four-space, we can move from the real part of the square root (x,
u, v) to the imaginary part (y, u, v). As we rotate from the real
part to the imaginary part of the square root, effectively we are
projecting into three-space the locus (cos(a) x + sin(a) y, u, v) as
the angle a changes from 0 to pi/2. The picture we see was first
described in the last century by the mathematician Bernhard Riemann,
and it is known today as the Riemann Surface of the Square
Root.

To observe this, play the movie
Similarly we can rotate from the graph of the cubing function to the
graph of the cube root relation z = w^1/3. In the case of the real
cubing function, there was an inverse function since every real number
has a unique real cube root. On the other hand, every complex number
other than zero has three distinct cube roots.


To observe this, play the movie
Next: Complex Exponential and
Logarithm Functions





