This paper addresses the question: Under what conditions is there an immerstion or an embedding f: M^2 -> E^3 of a closed surface M^2 into Euclidean 3-space such that there is a linear function on E^3, z:E^3 -> R, so that the composition zf: M^2 -> R has exactly three critical points, one of which may be degenerate? This problem for a smooth embedding f was proposed by H. Hopf in [6, p. 92]. A three critical point (3cp) smooth embedding is only possible in the case of a 2-sphere embedded as a "shoe surface" (see below).

When smooth immersions or polyhedral embeddings or immersions are considered, the results differ considerably. The following results are proven in this paper.
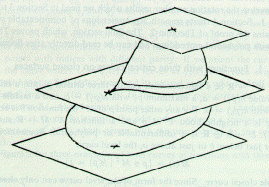
Theorem 1. There is a smooth 3cp immersion of the torus but there is no smooth 3cp immersion for any orientable surface of a genus greater than one.
Theorem 2. There is a smooth 3cp immersion of any nonorientable surface.
These immersions can be approximated by polyhedral 3cp immersions but in the polyhedral case we have an entirely different phenomenon:
Theorem 3. For any orientable surface except the sphere there is a polyhedral 3cp embedding into E^3.
These problems bear resemblance to the factorization problems studied by Haefliger in [3], where he answered the question of when an "excellent" mapping k: M^2 -> E^2 could be expressed as the composition of an immersion f: M^2 -> E^3 and the orthogonal projection p: E^3 -> E^2. Since for any surface M^2 there exist h: M^2 -> R with exactly three critical points, our work may be thought of as an attempt to factorize some such h as an immersion or embedding f: M^2 -> E^3 followed by an orthogonal projection into a line.
Section 5 gives examples of 3cp polyhedral embeddings which have been used as motivation for a study of the extensions of the idea of the degree of the Gauss spherical mapping to polyhedral embeddings in [1].
In Section 1 of this paper deals with arbitrary functions h with 3cp on surfaces. In Section 2 we examine those functions of the form h = zf and the rotation number results (which we need in Section 3 to prove Theorem 1) are derived. Section 4 gives the proof of Theorem 2, and discusses smooth 3cp immersions of nonorientable surfaces. The last section, which contains the proof of Theorem 3, deals with polyhedral embeddings and can be read directly after Section 1.
The following illustration (drawn by Cassidy Curtis) shows an immersion of the torus in three space that has exactly three critical points.
