 |
Applying the distance formula in the plane.
One of the greatest advantages of analytic geometry is that in a coordinate system of any dimension there is an explicit formula for the distance between two points, found by generalizing the Pythagorean theorem.
On a one-dimensional coordinate system, we may determine the distance between two points by finding the absolute value of the difference of their coordinates. The distance between the points labeled a and b is then |a - b|.
| ||
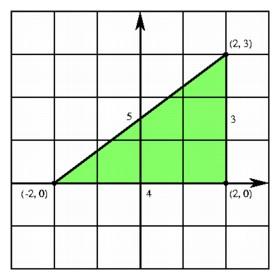
Applying the distance formula in the plane. |
In the plane, any two points (a, c) and (b, d) may be joined by a segment, and this segment is a diagonal of a unique rectangle with edges parallel to the coordinate axes. Because the base of this rectangle has length |a - b| and because the height of the rectangle is |c - d|, the Pythagorean theorem tells us that the length of the diagonal is given by ((a-b)2 + (c-d)2)1/2. For example, the diagonal of the unit square is the length of the line from (0, 0) to (1, 1), or 21/2.
The Pythagorean theorem can be extended to three-dimensional space by applying it to the length of the longest diagonal of a rectangular box. This diagonal is the hypotenuse of a right triangle having one side on the edge of the box and the other along a diagonal of a rectangular face of the box. We may apply the Pythagorean theorem once to get the length of the diagonal of the face and again to get the long diagonal of the box. The resulting formula for the three-space is a direct generalization of the formula in the plane. Instead of taking the square root of the sum of the squares of the two sides of a rectangle, we take the square root of the sum of the squares of the three sides of the rectangular box. In analytic geometry terms, this means that the distance between the point with the coordinates (a, b, c) and another labeled (d, e, f) is the square root of the sum of the squares off the differences of the corresponding coordinates, or ((a-d)2 + (b-e)2 + (c-f)2)1/2. For example, the length of the longest diagonal of the unit cube in three-space is the distance from (0, 0, 0) to (1, 1, 1), or 31/2.
| ||
To find the distance formula in three-space, we apply the planar distance formula twice, once to find the length of the diagonal of one of the faces, and then to find the hypotenuse of a right triangle having this diagonal and an edge of the cube as its sides. |
The generalization of the distance formula to higher dimensions is straighforward. By applying the Pythagorean theorem to a succession of planar triangles with sides given by edges or diagonals of the hypercube, the distance formula expresses the distance between two points as the square root of the sum of the squares of the differences of the coordinates. Thus the length of the longest diagonal of a unit hypercube is the distance between (0, 0, 0, 0) and (1, 1, 1, 1), namely 41/2 = 2.
| Coordinates for the n-Simplex | ||
| Table of Contents | ||
| Coordinates and Axes |