 |
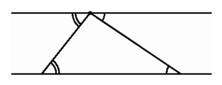
Once we can draw a unique line through one vertex of a triangle not meeting the line containing the opposite side, we can use alternate interior angles to see that the sum of the angles of a triangle is the same as a straight angle, 180 degrees.
For well over two thousand years, people had believed that only one geometry was possible, and they had accepted the idea that this geometry described reality. One of the greatest Greek achievements was setting up rules for plane geometry. This system consisted of a collection of undefined terms like point and line, and five axioms from which all other properties could be deduced by a formal process of logic. Four of the axioms were so self-evident that it would be unthinkable to call any system a geometry unless it satisfied them:
1. A straight line may be drawn between any two points.
2. Any terminated straight line may be extended indefinitely.
3. A circle may be drawn with any given point as center and any given radius.
4. All right angles are equal.
But the fifth axiom was a different sort of statement:
5. If two straight lines in a plane are met by another line, and if the sum of the internal angles on one side is less than two right angles, then the straight lines will meet if extended sufficiently on the side on which the sum of the angles is less than two right angles.
| ||
Once we can draw a unique line through one vertex of a triangle not meeting the line containing the opposite side, we can use alternate interior angles to see that the sum of the angles of a triangle is the same as a straight angle, 180 degrees. |
Because this axiom was much more complicated than the previous axioms, it seemed more like a theorem than a self-evident proposition. Since all attempts to deduce it from the first four axioms had failed, Euclid simply included it as an axiom because he knew he needed it. For example, some axiom like this one was necessary for proving one of Euclid's most famous theorems, that the sum of the angles of a triangle is 180 degrees. Mathematicians found alternate forms of the axiom that were easier to state, for example:
5'. For any given point not on a given line, there is exactly one line through the point that does not meet the given line.
This form of the fifth axiom became known as the parallel postulate. Although it was simpler to understand than Euclid's original formulation, it was no easier to deduce from the earlier axioms. The attempt to deduce the fifth axiom remained a great challenge right up to the nineteenth century, when it was proved that the fifth axiom did not follow from the first four.
The great advantage of expressing geometry as an axiomatic system was that it no longer was necessary to memorize long lists of independent facts about the nature of the universe--one only had to know a small set of axioms, and by applying to them the rules of inference, one could reconstruct the entire collection of geometric truths.
There was little doubt that the Greeks were attempting to describe a real world when they formulated their geometry, even though it might have been an ideal sort of world, realized only abstractly "in the mind of God." Many mathematicians, now as well as in the distant past, believe that the complete structure of mathematics is something that exists in itself and that it is only gradually discovered by human beings laboring to uncover its mysteries. Even though the framers of the early axiom systems would refer to point and line as undefined terms, they fairly clearly thought of them as real objects, and they thought that the system they were developing was a progressively more and more elaborate and accurate description of the real world. The progress of algebra, on the other hand, was not quite so settled, and people accepted changes in viewpoint there more readily than in the very traditional field of geometry.
| Noncommutative Algebra | ||
| Table of Contents | ||
| Introduction |