 |
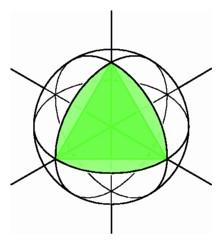
A spherical triangle can have three right angles beetween its pairs of great circle sides, even though the triangle with straight sides determined by the same vertices has angles of 60 degrees.
The greatest mathematical thinker since the time of Newton was Karl Friedrich Gauss. In his lifetime, he revolutionized many different areas of mathematics, including number theory, algebra, and analysis, as well as geometry. Already as a young man, he had devised a construction for a 17-sided regular polygon using only the traditional Euclidean tools, the straightedge and compass. His most significant contributions to geometry came in his analysis of surfaces, and this analysis played an important role in the understanding of non-Euclidean geometries.
Gauss was a surveyor, mapping out large areas of Europe, and he was an astronomer, studying phenomena in the heavens. In his land-based job, he triangulated areas, dividing them up into regions bounded by three of the shortest paths available on the surface of a sphere, namely great circle arcs. In his astronomical endeavors, he again used triangles to estimate distances, but this time the shortest paths available were the paths of light rays. In 1825 and again in 1827, Gauss combined insights from these fields to develop two ways of organizing information about surfaces, as intrinsic or extrinsic.
To appreciate the nature of the two approaches, he suggested a dimensional analogy--imagine what kind of geometry would be experienced by flatworms, two-dimensional creatures constrained to slide around oil a surface. Although we three-dimensional beings are bound by gravity to spend most of our time moving along the surface of our planet, we can at least occasionally overcome that superficial limitation, as when we dig or jump to avoid obstacles. But the flatworm, unable to move up or down out of a surface, is virtually confined to a two-dimensional existence. How would an intelligent flatworm describe the geometry of its universe? If the surface were a flat plane like Flatland, the inhabitants would develop ordinary plane geometry, and as part of that geometry they would discover that the sum of the angles of any triangle was 180 degrees. But what if they lived on a very large sphere, so large that the curvature was not apparent to the creatures sliding along it? If they measured a small triangle, the angle sum would be close to 180 degrees, but for large triangles the results might be quite different. The geometry discovered by the flatworm would be the intrinsic geometry of a surface; this geometry depends only on those measurements made along the surface.
The extrinsic geometry of a surface depends on the way a surface sits in space, and that is the geometry we would see in looking down upon the flatworm's universe. Guided somewhat by his studies of astronomy, Gauss referred the geometry of the surface to the set of directions on the celestial sphere. Each point of a smooth surface has a closest approximating plane, the tangent plane. For each point on the surface, Gauss found a corresponding point on a unit sphere such that the tangent planes at the two points were parallel. By this means, Gauss defined what he called the spherical image mapping on a surface, one of the most powerful means of studying the way a surface curves in space.
The most surprising and powerful theorems of Gauss are the ones that relate the intrinsic and the extrinsic geometry of a surface. One of his biggest discoveries was that the extrinsic curvature related to the Gauss mapping could be determined from the intrinsic geometry, just by making measurements along the surface. The flatworm surveyor could discover crucial facts about the shape of its universe without ever leaving its superficial environment. Like ourselves, the flatworm would be able to assign a distance to any path and to define the distance between two points as the shortest length among all paths joining the points. Just as we measure angles between rays, it could measure the angle between a pair of shortest curves emanating from a point, and it could calculate the sum of the angles of a triangle just as we do. The flatworm's answer, however, might be totally different from ours. If we start with three points on the flatworm's universe, we can take a shortcut through space and connect them by straight line segments, and the angles of the triangle we obtain will sum to 180 degrees. The flatworm, on the other hand, might claim that the sum of the angles is not constant and that it depends on the size of the triangle.
| ||
A spherical triangle can have three right angles beetween its pairs of great circle sides, even though the triangle with straight sides determined by the same vertices has angles of 60 degrees. |
Consider the particular case where the flatworm is confined to the surface of a sphere. He could construct a large triangle on the sphere running from the north pole to a point on the equator, then one-quarter of the way around the equator, and back to the north pole. Each of the angles of this spherical triangle is 90 degrees, so the angle sum is much greater than 180 degrees. For us who can leave the surface of the sphere to connect the points in space, the north pole and the two points on the equator form an equilateral triangle with each angle 60 degrees.
The geometric study of the sphere has a very long history, but by and large it was considered a subtopic in solid geometry. People spoke about great circle arcs, and they even knew in some sense that these represented the shortest paths on the surface of the globe. But they did not think of them as the same sorts of objects as the segments that provided the shortest distances in plane geometry. In ancient times, Ptolemy certainly knew that three great circle arcs forming a spherical triangle would determine angles adding up to more than 180 degrees, and in fact he was able to prove that the bigger the area of the triangle, the larger the angle sum. With proper choice of units this relationship could be made explicit: the area of a triangular region on the sphere is precisely the amount by which its angle sum exceeds 180 degrees. Why didn't Ptolemy realize that this was an example of a non-Euclidean geometry, where the important Euclidean theorem that the angle sum equals 180 degrees simply does not hold? The answer is that he did not think of the relationships among points of a sphere and great circle arcs as a geometry. To qualify as a geometry, a system would have to have elements corresponding to points and lines, and the first four axioms would have to be satisfied. The system consisting of points on a sphere and lines given by great circle arcs did satisfy the third and fourth axiom, and even the second if we interpret it correctly, but it did not satisfy the first axiom. Although two nearby points on the sphere determine a unique great circle arc, there are point pairs for which this is not true. More than one great circle arc joins the north and south poles, and in fact there are infinitely many half-circles of longitude joining these two points, all of the same length. Thus spherical geometry did not qualify as a non-Euclidean geometry, although later on in this chapter we will see that it was closely related to one.
In the early part of the nineteenth century, mathematicians in three different parts of Europe found non-Euclidean geometries--Gauss himself, Janós Bolyai in Hungary, and Nicolai Ivanovich Lobachevski in Russia. Each of them realized that it was possible to construct a two-dimensional geometry with points and shortest distance lines satisfying the first four axioms of Euclidean geometry, but not the fifth. The parallel postulate required that for any given point not on a given line, there is exactly one line through the point that does not meet the given line. There were two ways for this postulate to fail--if every line through the point meets the given line, or if there were two or more distinct lines through the point not meeting the line. The inventors of non-Euclidean geometry found systems based on both alternatives to the fifth axiom.
| ||
The alternative to the fifth axiom in hyperbolic geometry posits that through a point not on a given line, there are many lines not meeting the given line. |
The alternative axiom stating that there could be more than one line through a given point not meeting a given line led to hyperbolic geometry. The theorems deduced bv Bolyai and Lobachevski seemed quite strange, but they were as consistent as Euclidean plane geometry. The diagrams that accompanied their demonstrations certainly did not look like those in Euclid's text, and mathematicians searched for some visual representation that could make the new geometry easier to comprehend. One of the most successful expositors of this geometry, in England as well as in his native Germany, was the scientist Hermann von Helmholz. Appealing to the same thought experiment introduced by Gauss he used the dimensional analogy to explain a way of imagining a non-Euclidean two-dimensional geometry.
Helmholz asked his readers to consider a two-dimensional creature constrained to slide along the surface of a piece of marble statuary, measuring lengths of curves and sizes of angles. For example, a flatworm living on the surface of a cylindrical column would decide that for any region bounded by three shortest distance curves the angle sum would be 180 degrees, just the way it is on a plane, but if the column were in the shape of a long trumpet, the intrinsic geometry would be very different. The surface he suggested was a pseudosphere, invented by the Italian geometer Eugenio Beltrami. Although this surface had a sharp edge, it still illustrated most of the important properties of hyperbolic geometry, a geometry satisfying the first four axioms, but not the fifth. For any point and any shortest line, there were many lines through the point not meeting the line, and every triangle on the surface had an angle sum strictly less than 180 degrees!
The alternative axiom that every line through a given point would meet any other line led to elliptic geometry. This case was reminiscent of the geometry of the sphere, where every two great circles necessarily meet. The trouble with spherical geometry is that its straight lines meet twice. The radical solution was to throw away half the points of the sphere and just use the points in the southern hemisphere, below the equator. If the points of the southern hemisphere were the points of the geometry, and great circle arcs were the lines, then any two points did determine a unique line. The first axiom was saved. The third and fourth axioms still held, and the fifth certainly did not since there were triangles in the southern hemisphere having angle sums greater than 180 degrees.
But there was a new problem--the second axiom failed because the great semicircles lying in the southern hemisphere came to a dead stop when they reached the equator, and the second axiom requires that any line be indefinitely extendable. This difficulty was overcome by another radical suggestion: in addition to the points of the southern hemisphere, use half of the points of the equator, say those lying in the eastern hemisphere. When a point moving along a great circle arc in the southern hemisphere reaches the equator, it jumps instantly to the opposite point on the equator and continues to move along the great circle arc! In order for this procedure to work, we must consider the point on the equator at the prime meridian, with 0 degrees longitude, to be the same as the point on the international date line, with 180 degrees longitude. The amazing thing was that this idea worked. Using half the points on the sphere, it was possible to construct a geometry with great circle arcs as straight lines such that the sum of the angles of every triangle was greater than 180 degrees.
| ||
A model of elliptic geometry is given by the southern hemisphere with opposite points on the equator attached together. |
In elliptical geometry, it is as if every pair of antipodal points on the sphere represents the same point, and we only pay attention to the one lying in the southern hemisphere. The geometry is reminiscent of the geometry of lines through the origin in three-space, which we considered in Chapter 7. There we identified each line with the pair of antipodal points at which it meets the unit sphere. Thus the new interpretation of hemispherical geometry is associated with the geometry of lines, as well as with projective geometry.
This modification of spherical geometry had some weird consequences near the equator. In the new geometry, each point on the equator was considered to be the same as its antipode, directly on the other side of the sphere. When people tried to visualize this, they could easily attach opposite points together by wrapping the equator around itself, and they could even wrap together a small strip made by including part of the surface near the equator. But in order to do this it was necessary to introduce a twist, and when people tried to extend the construction over the entire southern hemisphere, they failed. The new geometry worked all right--it did not depend on being able to put it together in three-dimensional space. Fortunately by this time mathematicians knew of a place where the new geometry could be built, and that was in the fourth dimension.
| ||
Each point of the equator can be attached to its antipodal point by giving the equator a twist, then wrapping it around itself. |
| Three-Dimensional Non-Euclidean Geometry | ||
| Table of Contents | ||
| Noncommutative Algebra |