
Q: What size fence should I use when graphing 3D functions?
A: Many functions can be analyzed best over the 2x2x2 "unit" box: -1 < x,y,z < 1. However, certain functions may be easier to analyze over a larger fence. Take, for example, "Twin Peaks," f(x,y) = -x4 + 2x2 - y2. When analyzed over the unit box it appears to be a saddle function quite similar to f(x,y) = x2 - y2:
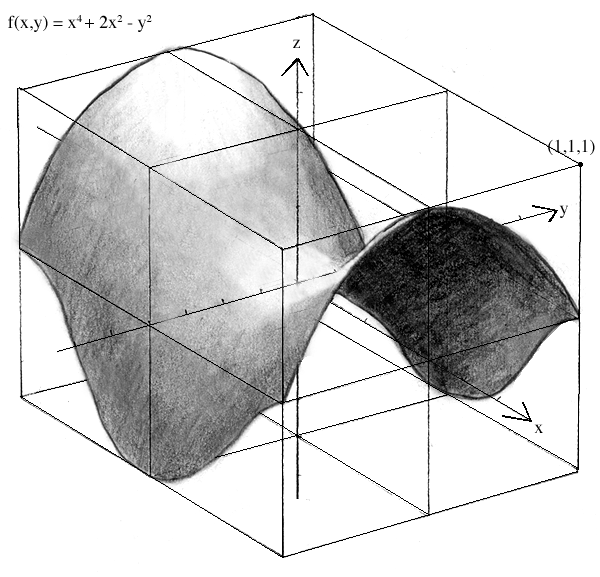
However, upon further analysis of the function's slice curves we may conclude that there is crucial information left out of the above graph.
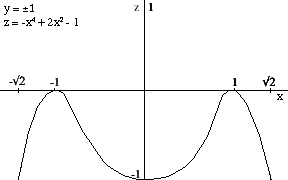
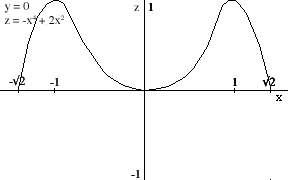
Slice curves y = 1, -1 (above left) and y = 0 (above right) contain critical points at x = 1, -1. Here the graph changes direction and proceeds downwards. We find that the graph hits the x axis when x = 21/2, -21/2, so perhaps we should extend our fence: -21/2 < x,y < 21/2:
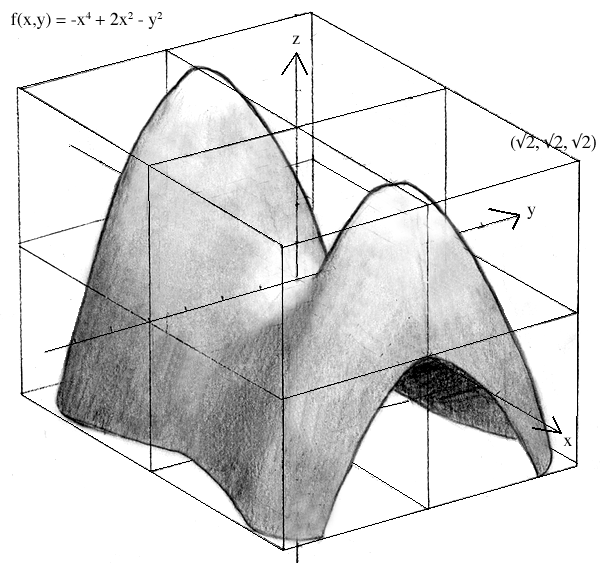
As you can see, using a larger box (or rather a smaller scale) allows us to see the true shape of the function, as well as to understand its name. Remember that this is always an option when graphing.