
Q: What size fence should I use when graphing 4D functions?
A: Just like 3D functions, 4D functions often tend to be most informative inside the unit fence. However, you must make sure that the level sets you have chosen allow you to see the full shape of the graph. As with 3D functions you should be careful not to jump to conclusions just because your function seems to give its critical information inside the unit fence. Take f(x,y,z) = sin(x)sin(y)sin(z) for example. When analyzed over the unit fence it appears to be quite similar to a smaller version of f(x,y,z) = exyz:
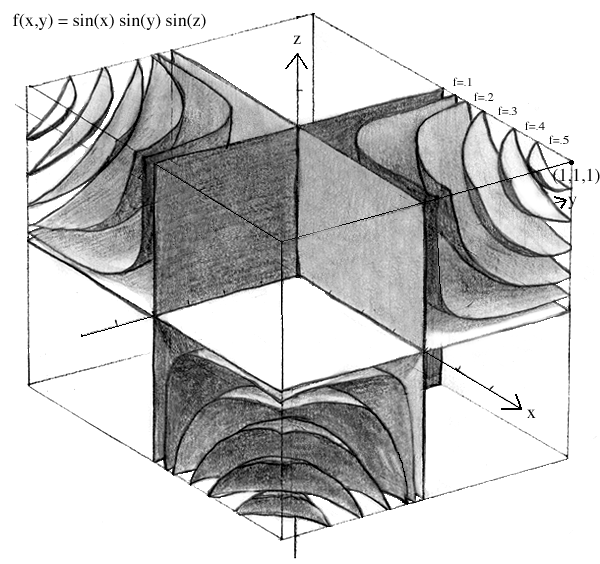
However, we know that the sine function is periodic, and thus must repeat itself in some way, while f(x,y,z) = exyz is not periodic. Furthermore, all trigonometric functions should be analyzed over some multiple of a "trigonometric" fence: -pi < x,y,z < pi:
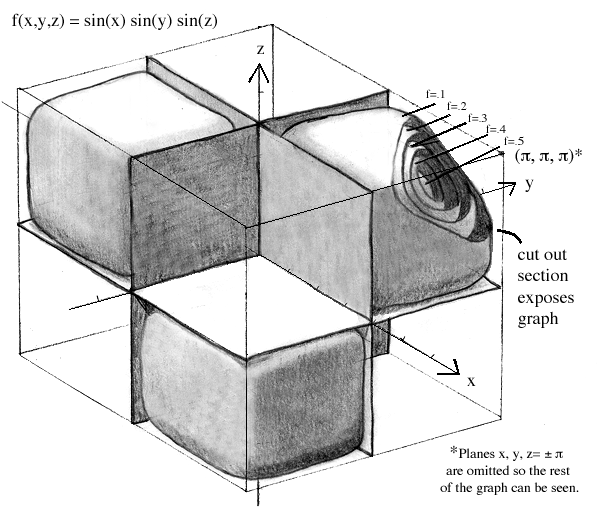
As you can see, using a more appropriate fence allows us to understand the true nature of the function.