
When graphing a function using the fence method it is important to draw its slice curves properly. Tips on correctly mapping slice curves onto fences follow:
PART I.Rectangular Fences
The simplest fence to use is a rectangular, or box-shaped fence:
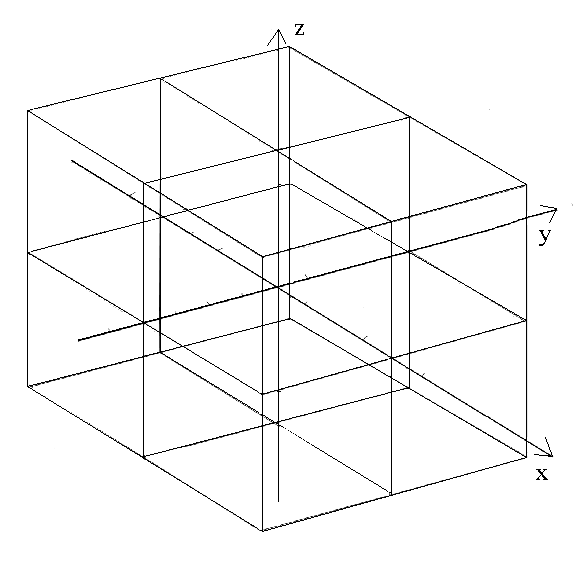
Mapping slice planes onto a rectangular fence is fairly simple:
(We will use f(x,y) = x2 - y2 as an example)
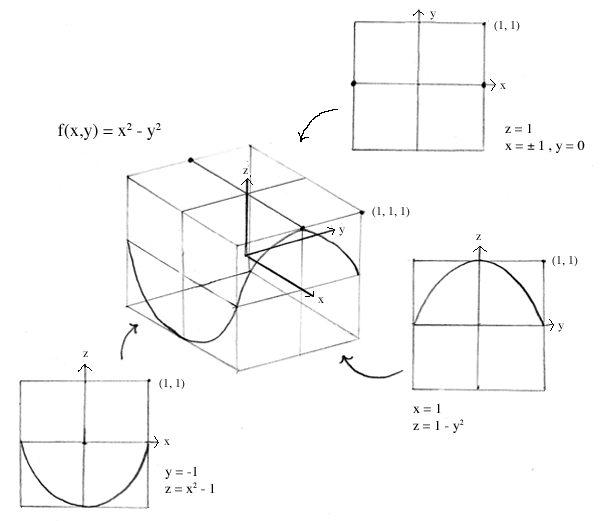
Step 1. Draw out all slice curves on square 2D graphs.
Step 2. Imagine that each square graph is stretched into the diamond shape of the plane onto which it is to be mapped. An alternative way to achieve the same effect is to mentally rotate the 2D slice curve around into 3-space. This method is at first more confusing, but once you have mastered it, you can easily skip the step of drawing the 2D graph.
Step 3. Draw this newly sketched graph into the diamond-shaped plane. It may help to imagine the stretching of each quadrant separately if you are having trouble seeing where each part of the graph should go.
PART 2. Cylindrical Fences
Another good time to use mental rotation of slice curves is when you are graphing a function over a cylindrical fence:
PICTURE OF CYLINDRICAL FENCE GOES HERE
It can be a bit tricky to map a slice curve taken at a fixed radius onto a cylindrical fence, since it is a curvy surface which overlaps when drawn. Here's one way to go about it:
(We will use f(x,y) = x2 - y2, translated into polar coordinates: f(r,t) = r2cos(2t) as an example.)
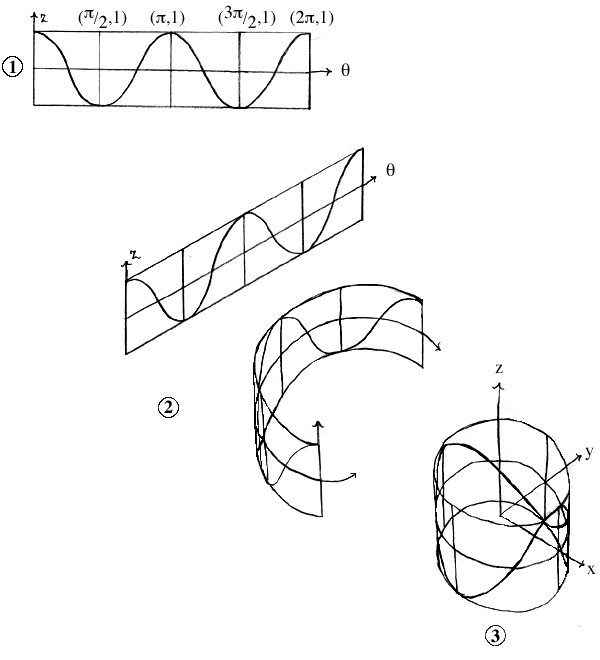
Step 1. Draw a flat graph of the slice curve of f(r,t) where r = 1 (or any other fixed value) and 0 < t < 2pi.
Step 2. Imagine curling this flat graph up into 3-space until the t = 0 edge and the t = 2pi edge meet.
Step 3. Draw this curve on the r = 1 fence of your graph. This is the tricky part. One way to make sure you get it right is to graph points on the r = 1 cylinder where f = -1, 0, 1. That way all you have to do is draw in the curvature properly. Again, it also may help to look at each quadrant separately if you're still confused.
Step 4. Take rectangular slic curves at t = 0, pi and at t = pi/2, 3pi/2. (See PART I. for info on rectangular mappings.)