
Q: What is the best method to use when graphing 3D functions and why?
A: Graphing using the fence method is usually easier and often offers more information than graphing using the level set method.
Graphing using level sets can certainly be useful, especially for functions which can be translated easily into polar coordinates. Take f(x,y) = x2 + y2, translated to f(r,t) = r2, for example. With this function it is easy to solve for many level sets. Here, solving for z = 0, 1, 4, 16 gives a fairly good approximation of the function:
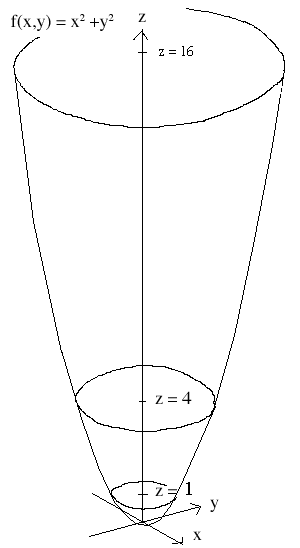
With most functions it is hard to obtain these multiple level sets without solving some ugly equations. Graphing with the fence method rarely requires you to solve messy equations. The fence method also gives a more complete view of the surface being analyzed. Using the fence method we can easily see that the surface is a paraboloid, whereas we could only guess at its parabolic nature using level sets:
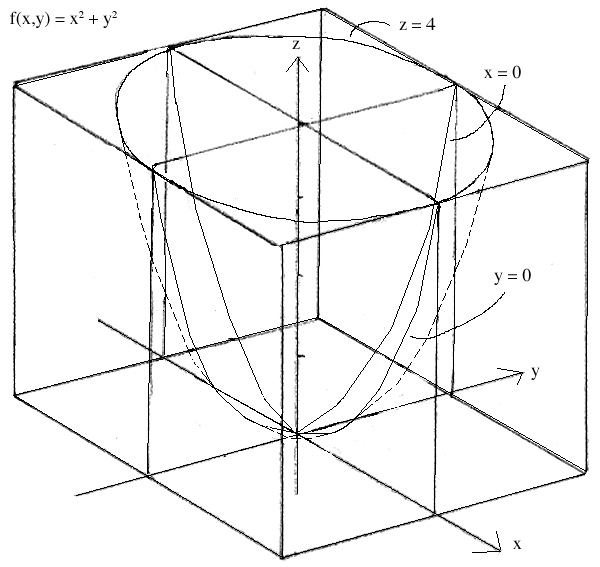
To correct this glitch we could have taken x or y fixed level sets, but it is usually to our advantage to take x, y, and z fixed level sets all at once. This is essentially what the fence method does. With the fence method, we take level sets, or slice curves, at strategic values of x, y, and z, thus cutting down graphing time and giving us a more accurate surface skeleton from which we may then proceed to interpolate the shape of the entire surface.