MARTIN GARDNER AND "FLATLAND"
Four times in major essays in the Scientific American, Martin Gardner
specifically treated the dimensional analogy, as introduced by Edwin
Abbott Abbott in the 1884 classic "Flatland". In the first of
those pieces, entitled "Flatlands", he presented a puzzle that has
surfaced once again as
a central feature of the latest animation of that book, "Flatland the
Movie", where the two-dimensional protagonists confront a
three-dimensional
cube with its center fixed in their plane as it rotates continually in
three-space. Of course Flatlanders can only see the slices of
this object
in their universe, sometimes a square, other times a rectangle or a
rhombus or, most surprisingly, a hexagon. Years ago in one of his
Scientific
American columns, Martin Gardner challenged his readers to determine
which of these "central sections of a cube" would have the greatest
area. The somewhat surprising answer was given in the next issue.
Now that the same problem reappears in animated form in this new
version of the Flatland story, teachers have a new opportunity to
explore questions about these central slices with their students.
As part of this gift for G4G8, we present selections from pedagogical
materials being prepared to go along with the DVD of this animation,
for use by teachers in middle school, secondary school, college and
university, and for general audiences.
Special thanks go to Brown University undergraduate assistants Michael
Schwarz and Tan Van Nguyen who created the Java animations using
locally developed software created over the years by other
undergraduates, supported by funds from Brown University and from the
National Science Foundation.
HEX EXPLORES THE AREA 33H CUBE SLICES
When Hex goes to Area 33H to see the Old Ruins for
herself, she
says,
"I was right!" Visitors many centuries ago had left
a sign so
that people in Flatland might come to know the existence
of the Third
Dimension. Although Hex could not appreciate it when she
first came to
that monument, she was seeing a cube rotating in space
about its
center. Of course since she was in the plane, she couldn't see
the whole cube all at once, but she could see the slices of the cube
sitting in Flatland in front of her. By observing
all of those
slices, she could begin to understand quite a bit about
this
mysterious cube.
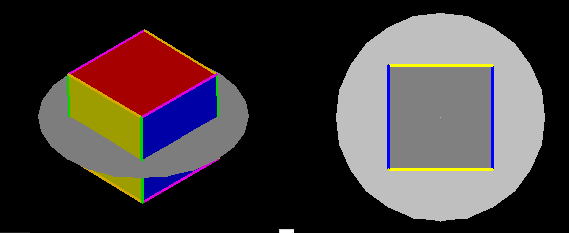
Hex could keep track of different slices, and
we can too, especially
if we use color. In the movie, all of the square sides of
the cube
have the same color. It will help us to describe our observations if
we color the six sides of the cube, with two opposite square colored
red, two opposite sides colored yellow, and the remaining
two opposite
sides colored blue.


As long as we are coloring the square faces of the cube,
we
might as
well color the edges too. An edge where a red square meets a blue
square we can color purple, and similarly we can color orange each edge
where a red square meets a yellow square. What color should an
edge where a blue square and a yellow square meet? How many of
the edges will be colored purple? How many orange? How many
green? How many segments are there all together?
We are now ready to study the horizontal slices of
the
colored
cube. The easiest slice to understand is a square. If we
hold a cube so that one of the square faces is horizontal,
then the
slice of the cube that lies in the horizontal plane
through the center
will be a square. If the horizontal squares are red, then the
blue and yellow squares are all sliced the same way, producing a square
with two blue edges and two yellow edges. What are the other
possibilities?


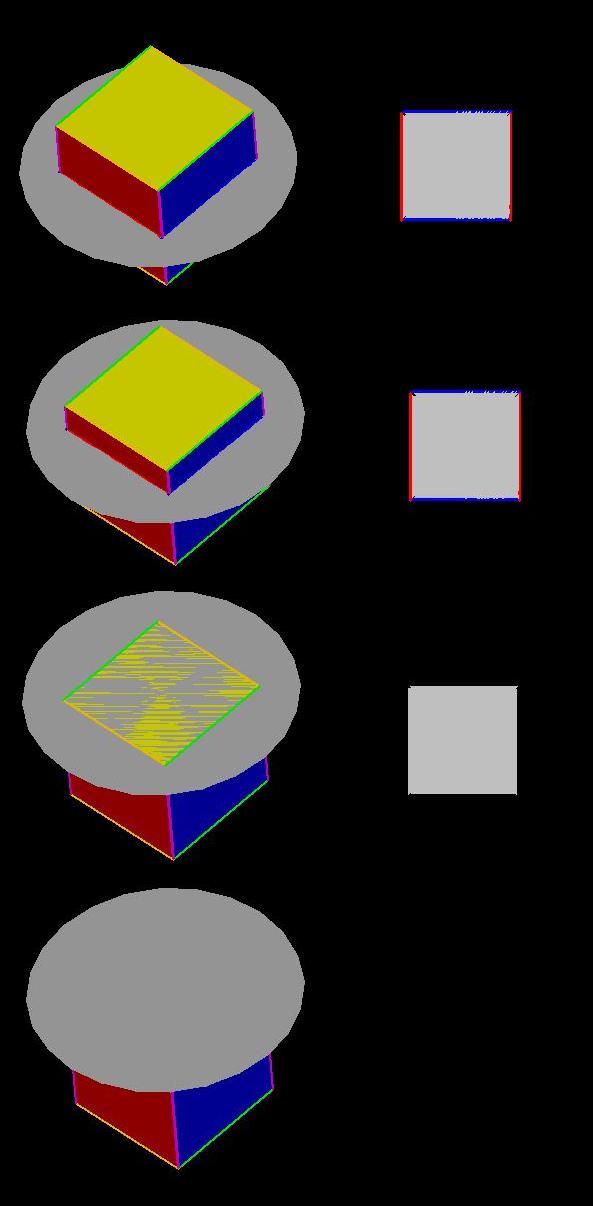
Now we want to see what happens if the cube starts
to
rotate. If we start with a cube with red squares on the top and
bottom and with yellow square in the front and back, then
we can
rotate it so that the yellow squares stay in the front and
back.
Each of the yellow squares rotates about its center. At the start
of the rotation, the slices of these horizontal squares will be yellow
segments with green endpoints. The other two edges of the
horizontal slice of the cube are blue with green endpoints. As
the cube rotates about the centers of the two vertical yellow squares,
we obtain a quadrilateral that is no longer a square but a rectangle
with two blue segments and two yellow ones. The two blue segments
stay the same length while the yellow segments grow larger until the
square has rotated one-eighth of the way around and the horizontal
slice segments are now the diagonals of the yellow squares. At
this point, the horizontal slice of the cube is a rectangle with two
long yellow segments and two purple segments of the original cube,
where a red square meets a blue square.


If we continue to rotate, then we will not
slice the
blue squares any more, and we now start to slice the red squares.
We get rectangles with two red segments that stay the same length while
the yellow segments are getting smaller. By the time that the two
blue squares are horizontal, the central slice of the cube is a square,
with two sides red and two sides yellow. What will happen if we
continue? When do we get back to the starting point?
If we stop the rotation when two blue squares
are
horizontal, the slice will be a square with two segments yellow and two
red. What will happen if we not rotate the cube so that the two
red squares rotate about their centers?
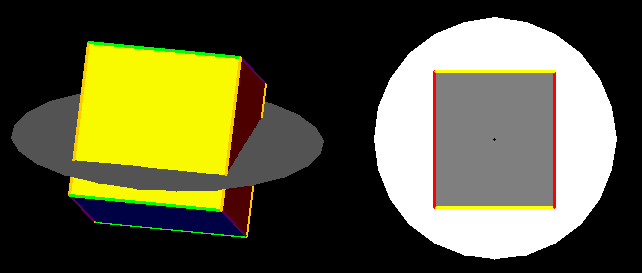
We know that the perimeter of the rectangle
is the
sum of the lengths of its four sides, and the area of a rectangle is
the length of one pair of sides multiplied by the length of the
other. Which of the horizontal rectangles has the smallest
perimeter and which has the largest? What about the areas of the
rectangular horizontal slices as the cube rotates?
Describe what happens if we start with red
squares
horizontal and rotate about the centers of the two blue vertical
squares. What can we say about the shapes and colors of the
slices, and what about their perimeters and areas? (It is
possible to estimate the perimeter and the area by measuring two sides
of each rectangle. Students who know about the Pythagorean theorem can
find the perimeter and area of the largest of these slices in terms of
square roots. Students who know trigonometry can express the
perimeter and area of a rectangular slice in terms of sines and cosines
of angles of rotation.)
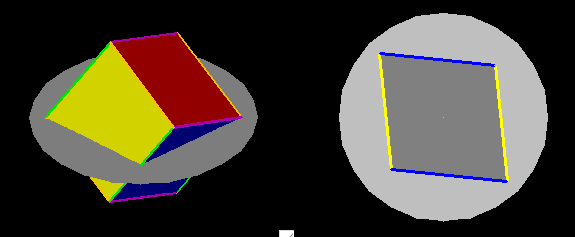
We continue our investigation of the central
slices
of a cube by
stopping when the horizontal slice is a rectangle with two purple edges
and two longer yellow segments. We now rotate the cube so that a
diagonal of this cube stays fixed. Which way we rotate makes a
difference. One way gives quadrilaterals with two yellow segments
and two blue ones and the other gives quadrilaterals with two yellow
segments and two red ones. Consider first the case where two
segments are blue and two are yellow. Since the two yellow
squares are parallel in space, when they are cut by the horizontal
plane, we have to get two parallel yellow segments. Similarly the
horizontal slices of the two parallel blue squares will be two parallel
blue segments. The quadrilateral slice therefore has to be a
parallelogram. At the beginning of the rotation, the yellow
segments of the parallelogram are longer than the blue segments, and
when the horizontal plane goes through the midpoints of a pair of green
edges of the cube, the yellow segments and the blue segments have the
same length. The slice of the cube is then a rhombus. Even
though this non-square rhombus would be considered an irregular figure
in Flatland, Hex can appreciate its symmetry.
What is larger, the perimeter of the rectangle or
the perimeter
of the
rhombus? What about the areas of these figures?
What happens to the rhombus as we continue the
rotation about
the
diagonal of the horizontal rectangle?
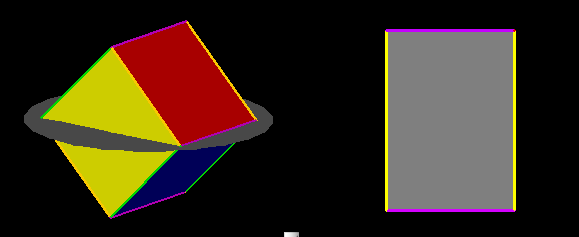
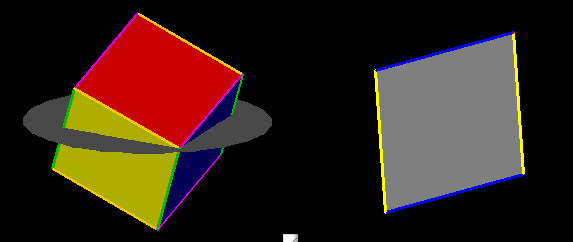
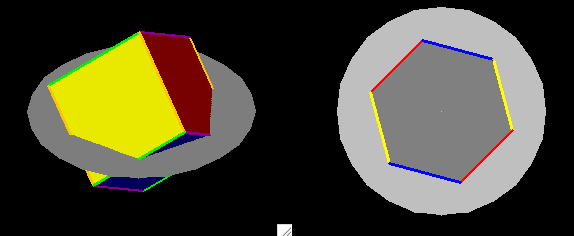
Naturally Hex is particularly interested in slices
that are
hexagons. Since the cube only has six square sides, we
cant get
more than six edges in any slice. Moreover, by the argument given
above, the segments in the central slices come in pairs of parallel
edges. As it happens, we can get hexagonal slices by can get some
of those by rotating a horizontal rhombus around its short
diagonal. If the rhombus has two blue segments and
two yellow
ones, then as the cube rotates, two small blue segments
will
appear. The slice has six edges, with opposite segments parallel
and colored the same. At one position as the cube
rotates, the
horizontal slice has all six segments exactly of the same
length, and
with all angles equal. We get this perfectly
symmetrical
hexagonal slice when the cube is positioned so that one of
its long
diagonals is vertical. For Hex, that is the most
satisfying
discovery--a slice of this mysterious cube from the third
dimension
can be a square, a rectangle, a rhombus, or, nicest of all, a hexagon
like herself.
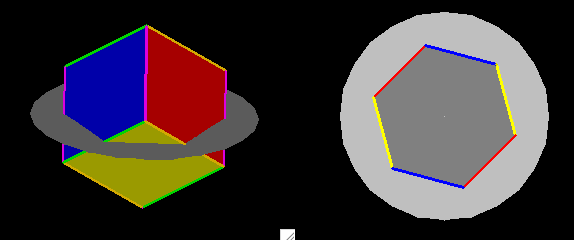
There is another way of getting to the regular hexagonal slice by
starting with the square slice that has two yellow segments and two
blue segments and four green vertices at the midpoints of the vertical
green edges of the cube. If we rotate about a diagonal of this
square, then at the beginning, we have to get parallelograms, by the
argument given above, and since the blue and yellow squares are treated
equally in this rotation, we have to get rhombi, all the way up to the
point where we have the largest rhombus, with two points at opposite
corners of the cube. If we continue the rotation, then small red
segments appear, as in the previous exploration, and ultimately these
have the same length as the blue and yellow segments. At this
point, all of the segments have the same length and all of the angles
are equal!
For those of us who live in three-space, another way of studying the
slices of cubes by planes is to keep the cube fixed and rotate the
plane. This change of viewpoints is relates to the idea of
relativity since we are interested in the relative positions of the
cube and the plane. We can determine the position of a plane
through the origin by seeing how it intersects a unit sphere---More
later!
SLICING CUBES AND HYPERCUBES IN "FLATLAND: THE MOVIE"
We have analyzed the slices that arise
when the horizontal plane through the origin slices a cube rotating
about its center that is fixed at the origin. Our approach up to
this point has been synthetic, without specific attention to the
formulas that the computer uses to determine the slices and to display
them. We now start with some elementary analytic geometry of
lines in the plane to show how to find slices of a square, and then how
to extend this approach to find slices of a cube in three-dimensional
space. As we will see, this approach generalizes even further to
allow us to investigate the slices by our three-dimensional universe of
a hypercube rotating in four-dimensional space with its center fixed at
a point in our world.
SLICING SQUARES BY LINES IN THE PLANE
Slicing squares throught the center is
an easy exercise. Whenever we slice a square with vertices (+-1,+-1),
we get a segment meeting the boundary of the square at two opposite
points. If the horizontal edges, with y = +-1, are red and the
vertical edges, with x = +-1 are blue, then the four vertices are
colored purple. Any non-vertical line ax + by = 0 will have slope
m = -a/b. The endpoints of the slice segment will be a pair of
purple vertices if m = +-1, a pair of blue vertices if |m| < 1 and a
pair of red vertices if |m| > 1.
More generally a line ax + by = e will
meet the four lines that determine the square in four points:
(1,(e-a)/b). (-1,(e+a)/b),((e-b)/a,1) and ((e+b)/a,-1). Exactly
two of these four points will be on the boundary of the square.
The only way for one of the points to be purple is if either (e-a)/b or
(e+a)/b is +-1. In particular both endpoints will be purple if e
= 0 and a = +-b. If |(e-a)/b| and |(e+a)/b| are both less than 1,
both endpoints will be blue, and if |(e-b)/a| and |(e+b)/a| are both
less than 1, then both endpoints will be red. We will have one
endpoint blue and one red if exactly one of the values |(e-a)/b| or
|(e+a)/b| is less than 1, in which case just one of the values
|(e-b)/a| or |(e+b)/a| is less than or equal to 1.
SLICING CUBES BY PLANES IN THREE-DIMENSIONAL SPACE
We can use this information to describe
the slices of a cube by a plane through the origin. If the cube
in 3-space has vertices (+-1,+-1,+-1), then the slicing plane ax + by +
cz = 0 meets the top square with z = 1, if at all, either in a vertex,
in an edge, or in a segment. If the top square is colored red,
with edges colored purple if y = +-1 or orange if x = +-1. The
intersection of the plane with the top red square will be either the
empty set or a vertex of the square or an edge of the square or a
segment joining two vertices of the square face. Whatever the
intersection is with the top square face, that same intersection occurs
on the opposite bottom face, i.e. if (x,y,1) is in the intersection on
the top, then (-x,-y,-1) is in the intersection on the bottom.
Moreover the segments on the top and
bottom faces will have the same length and be parallel.
A similar analysis shows that the
central slices of the cube will meet the two vertical blue faces, if at
all, each in a point, or a pair of opposite edges of the cube or in a
pair of congruent parallel blue segments, and the same is true for the
intersection with the pair of vertical yellow squares. The central
slices are then either parallelograms, or hexagons with three pairs of
opposite segments congruent and parallel.
Just as we sliced the square with lines
not through the origin, we can slice the cube will planes of the form
ax + by + cz = e. We will obtain either a vertex, or a triangle
with three edges of different colors, or a quadrilateral with exactly
on pair of parallel sides or a parallelogram or a pentagon with two
pairs of parallel edges or a hexagon with three pairs of parallel edges.
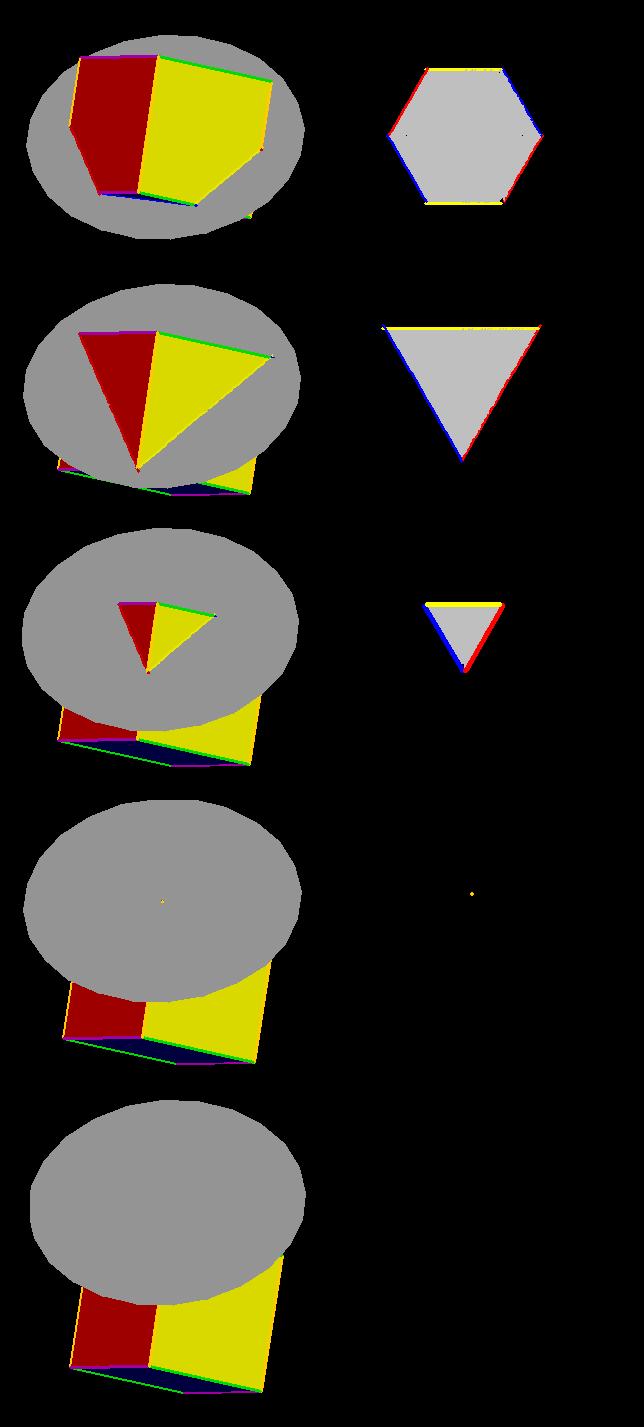
Off-Center Slices with a = 1, b = 0, c = 0
Off-Center Slices with a = 1, b = 1, c = 0
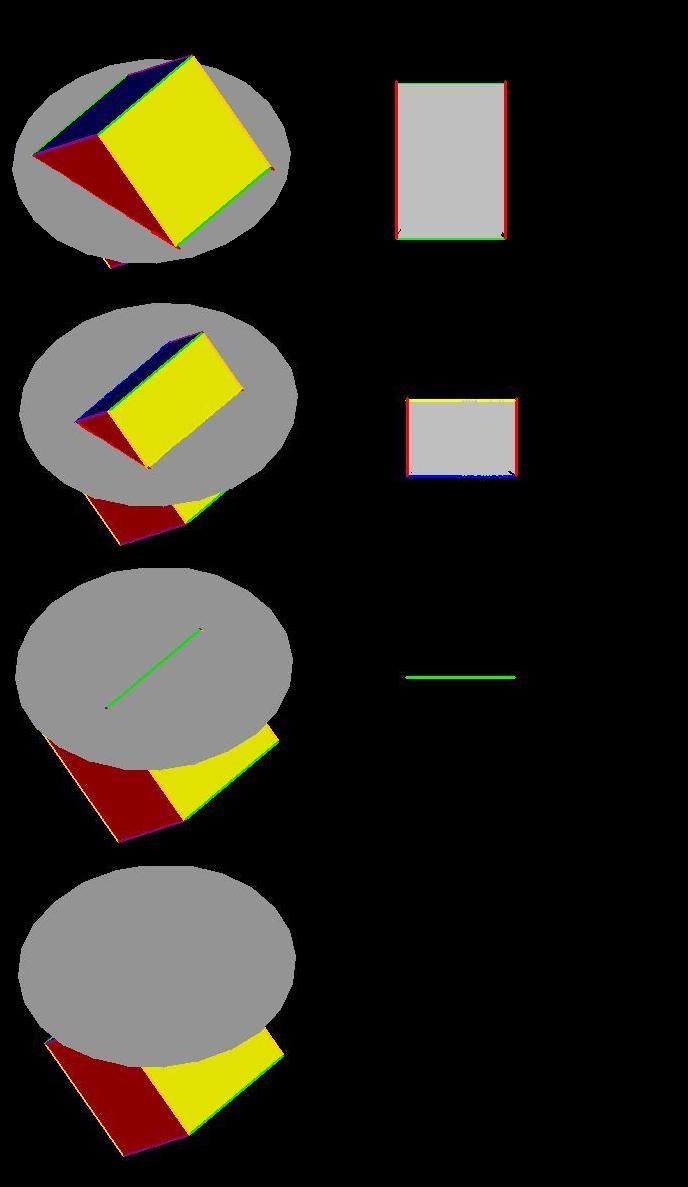
Off-Center Slices with a = 1, b = 1, c = 2

Off-Center Slices with a = 1, b = 1, c = 1
SLICING HYPERCUBES BY HYPERPLANES IN FOUR-DIMENSIONAL SPACE
These off-center slices of cubes will be
the building blocks of central slices of the hypercube with vertices
(+-1,+-1,+-1,+-1) by hyperplanes of the form ax + by + cz + dw =
0. The hyperplane will meet the hyperplane w = 1 in a plane of
the form ax + by + cz = -d, and this will slice the cube with w = 1 in
one of the forms described above. The intersection of the
hyperplane with the hyperplane w = -1 will be congruent to the slice
with the hyperplane w = 1, symmetrically situated with respect to the
origin. Similarly we will slice the cubes with z = 1 and z = -1
to find a pair of opposite vertices or opposite edges or congruent
convex polygons with three, four, five, or six sides, symmetrically
places with respect to the origin, and the same happens for the pair of
cubes with y = +-1 or with x = +-1. There will be at most eight
of these intersections, fitting together to form a convex polyhedron in
the 3-dimensional hyperplane.
If all we want to see is the set of
edges of this convex polyhedron, we can find the segments in its
boundary by slicing a square with two coordinates fixed at 1 or -1 by
the plane ax + by + cz + dw = 0. We will get 24 squares of this type
since there are six choices for two of the four coordinates and, for
each such pair of coordinate slots, two choices +-1 for the entry in
that slot. Note that the final figure will be symmetric with respect to
the origin, so any segment formed by slicing a square, say of the form
(1,-1,x,w) will have a congruent opposite segment with points of the
form (-1,1,-x,-w).
Rotation Giving Transition from Rectangular Prism Slice Hexagonal Prism
Slice
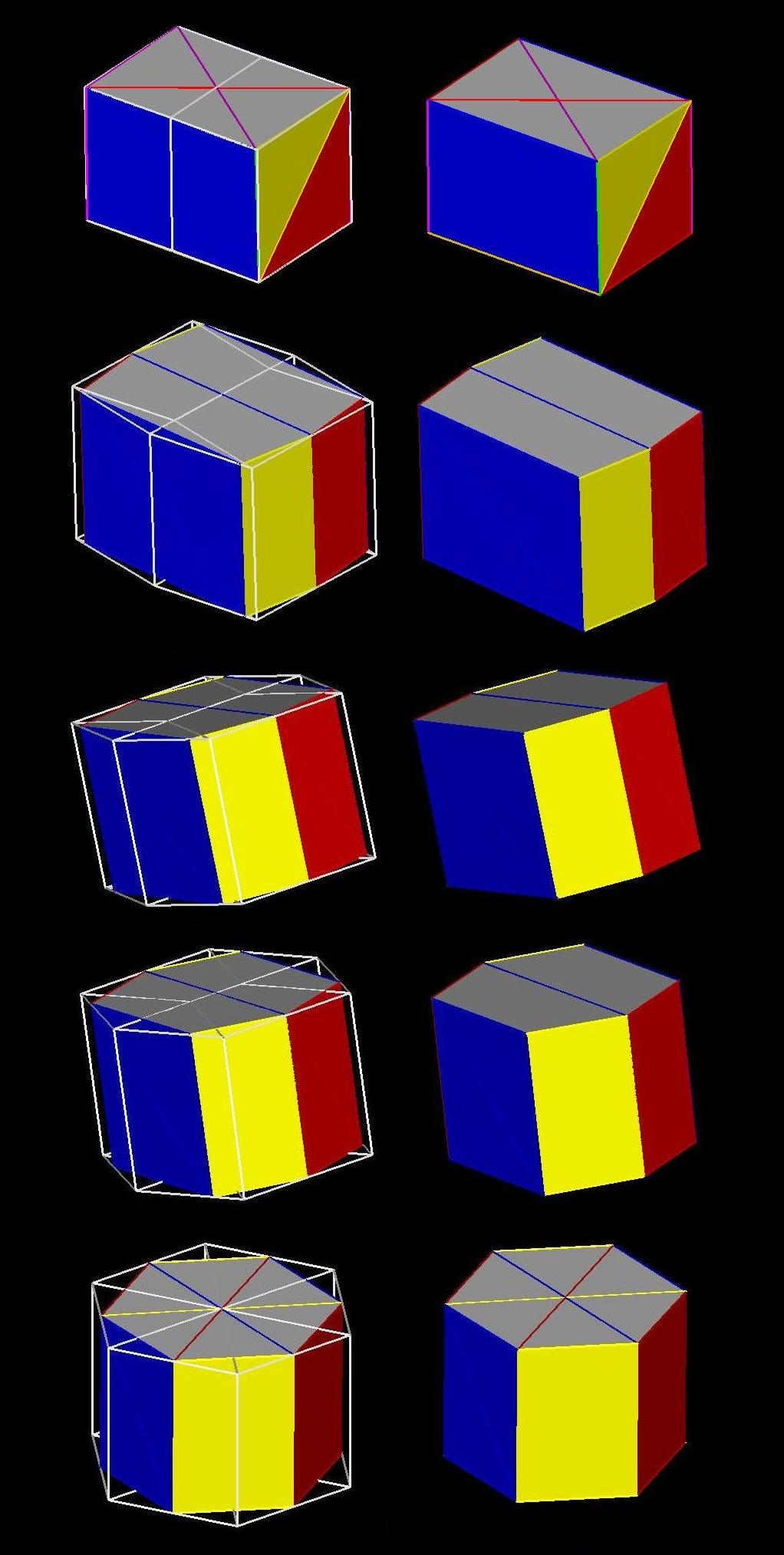
Rotation Giving Transition from Hexagonal Prism Slice to Octahedron
Slice:
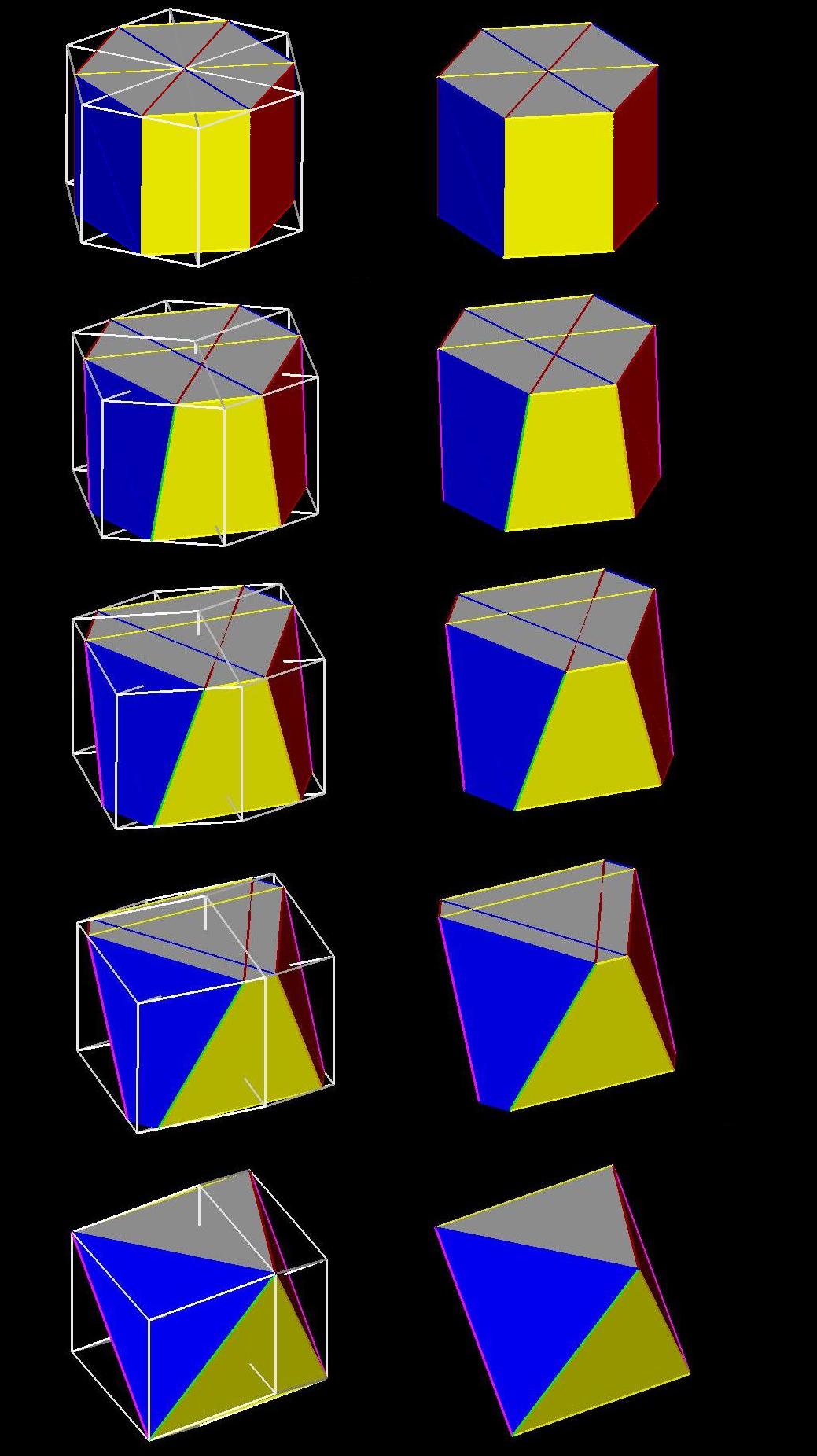
CONCLUSION
In "Flatland: the Movie", the final
sequence shows some views of projections of a hypercube but they do not
correspond to the slices of the cube by Flatland that are the basis of
the sign left by earlier visitors from the third dimension. The
images show perspective views of a hypercube being projected into
three-dimensional space instead of symmetrical three-dimensional slices
of a hypercube rotating about its center. Just as Martin Gardner
challenged his readers to find the central section of a cube with the
largest area, Spherius, as well as the viewers of "Flatland: the Movie"
will face the challenge of describing the slices by the hypercube in
our three-dimensional universe and of figuring out which one of those
hypercube slices has the greatest three-dimensional volume. It is
a problem that Martin Gardner will enjoy.












