A subdivision surface is animated by moving the points of the control mesh. No matter where they are positioned, the final surface is guaranteed to be smooth, thanks to mathematical results proved by scientists at Pixar Animation Studios..
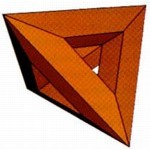    |
The first image shows the points and facets (collectively called the control mesh) used to create a subdivision surface.
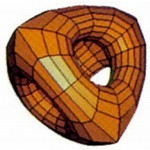
The second image shows the control mesh after one subdivision step. Each of the 24 facets of the control mesh has been split into 4 facets (for a total of 96 facets), and the points have been repositioned using a carefully constructed averaging process that Ed Calmull and Jim Clark created 20 years ago. (See "Recursively Generated B-spline Surfaces on Arbitrary Topological Meshes." Computer Aided Design, 10(6), 1978.) In the third image the mesh has been split and averaged once again, resulting in more facets.
The fourth image shows a final subdivision surface. The magic that guarantees that the final surface is smooth is tied up in the averaging process, most averaging methods create infinitely bumpy "tractal" surfaces. Recently, a rigorous mathematical proof of smoothness of the surface was constructed by Ulrich Reif (See "A Unified Approach to Subdivision Algorithm," Technical Report A-92-16. Universtaet Stuttgart. 1992). As the math has become better, the software for creating smooth animated surfaces has become simpler.
Conceptually, the final surface is the infinitely faceted model that results if subdivision is repeated forever. Of course, in practice one cannot subdivide forever, so we've developed methods that allow highly accurate images to be created after just a few subdivision steps. Some of those methods are in a technical paper published in the SIGGHAPH 93 Conference Proceedings: "Efficient, Fair Interpolation Using Catmull-Clark Surfaces," by Mark Halstead, Michael Kass, Tony DeRose.
|
|