Hyperspace theory (also called Superstring or Supergravity theory) begins with Einstein's General Relativity. In 1919, Theodr Kaluza, building upon relativity, made an astounding discovery: light and gravity can be unified and expressed with identical mathematics. This was the beginning of the unification of all physical laws, which is the ultimate goal of physics. There was only one catch. He needed an extra dimension. This fifth dimension, long recognized as mathematically plausible, had never before been seriously proposed as an actual component of reality. The usefulness of his theory was hard to deny; in five dimensions, there is "enough room" to accomplish the unification of gravity and light, which simply cannot be accomplished when trapped in four dimensional spacetime.

There is an obvious question to be asked at this point. "Where is the fifth dimension?" Kaluza's answer is clever, though suspiciously hard to test. He said that the fifth dimension is too small to see. The fifth dimension is contiguous with our four, but it is curled up, while the others are extended. To understand curled-up dimensions, imagine an ant living on a string (or a Linelander). For all its life, it is only aware of two directions: forward and backward. It lives in a one-dimensional universe. However, if you examine the string very closely, you find that it has a circumference; an extra dimension, curled up and wrapped back onto itself into a circle. If you could stretch this dimension, that is, make the circumference very large, the ant would be living on the two-dimensional surface of a cylinder. But when it's curled up, it effectively is undetectable by the ant, though it may serve as a medium for vibrations or other physical effects.

This Kaluza-Klein Theory (named after Kaluza and one of his students) was a curiosity for a while until people became disenchanted with its bizarre hypotheses and lack of concrete predictions. A common criticism was to ask why, if there could be one extra dimension, why not many? Just how many dimensions did this wacky theory have? For many years, people were content to leave gravity behind and work on examining the nature of subatomic matter via Quantum Mechanics.

Fortunately, in the 1980's, Kaluza-Klein came back with a vengence. The new wave of physicists supporting Hyperspace ("higher"-space) theories had an important element which was missing in the thirties: an exact prediction of the number of dimensions in our universe. By manipulating the formulae of Einstein, Riemann, and the like, they managed to unify all the forces of nature (gravity, the strong and weak nuclear forces, and the electromagnetic force, which includes light) in a single theory. How many dimensions did they need? Ten.

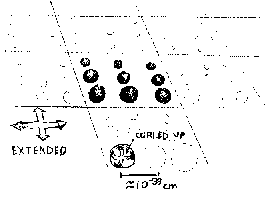
According to Hyperspace theory, each point in our four-dimensional universe conceals an additional six curled-up dimensions. The image at left provides insight on how this might be possible. Here we have a two-dimensional plane viewed at great magnification. At each point in the plane, there are the two curled-up dimensions of a sphere. In our universe, each point contains not a sphere, but a higher-dimensional object: a six-dimensional "Calabi-Yau Manifold." There is a very simple reason why we can't see these manifolds: they are less than 10^-33 centimeters across, much smaller than our most powerful microscopes can detect. Nonetheless, the movement of vibrating "strings" through these manifolds may be the source of all of physics.