Chapter 6 presents a good example of the connections between art and the sort of mathematics we're doing. The fact that our retinas are (at least in separation) two dimensional organs makes questions of perspective important; we seem to think we're moving around in three dimensions, and something about our visual input seems to reinforce this. It turns out that one of these things is perspective, as most paintings/drawings/other media consisting of variously colored rectangles which do not follow perspective may look unrealistic, or, as the example in the margin of page 125 illustrates, disorienting.
This brings to mind for me the cubists. One of the stated goals of their style of painting was to present their subjects more realistically, but not according to the realism of the viewer. Rather, they meant for their paintings to portray all of the subject, not just a perspective. While this may have been meant metaphorically, obviously there are dimensional implications of this idea.
On an organization note, I do not see why the section titled "Perspective Views of a Hypercube" was separated from the section on hypercube animations by the sections on Schlegel polygons/hedra. This seemed unnecessarily confusing and disorienting, as the sections do not really lead into each other clearly.
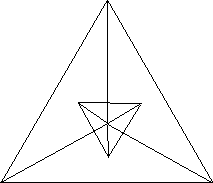
Nevertheless, the information on Schlegel polyhedra was quite interesting. One thing which jumped out at me was that if the shadows of the centers of each face's representation in the polyhedron was connected, one obtains something tantalizingly close to another Schlegel polyhedron, although not necessarily oriented the same as the special Schlegel polyhedra on page 117; for instance, we can imagine that the triangle in the center of this diagram of the tetrahedron is part of another tetrahedron dual to the original.

On reflection it was obvious why this was so; essentially, I had drawn the central projection of the dual to each regular polyhedron. This relationship should then also hold for the Schlegel polyhedra of the regular polytopes, and indeed it seems to looking at the pictures on page 118, with the same restriction that the duality is not as neat as it had been in the original figure.
This led me to wonder what would happen to take consecutive dualizations of these schlegel polyhedra/gons. Obviously, as with the higher dimension, the figure would get smaller. However, here there was also the added complication of losing information with each turn; each successive drawing shows fewer faces of the higher dimensional object, and eventually you run out of centers of faces to connect because there is only one face and only one center. Let us look at the cube. Connecting the centers of the faces in the diagram of a cube gives us something like this.
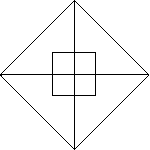
The figure can be seen as a square with all of its vertices connected; it can also be seen as an octahedron view from one of its vertices. This is is a possible Schlegel polygon of the octahedron, although not the one in the book. Notice, however, that this octahedron is not as helpful to us as the one in the book. In this diagram, the outside edge does not correspond to a face. In fact, not all of the faces are visible. We only see four faces in the plane because each face completely coincides with another. If we try to continue Schlegelizing this figure, we end up with part of a cube's Schlegel diagram: in fact, a single face. After this, we are stuck, since the face has only one center and there are no more edges to draw.
The other Schlegel diagrams behave similarly. I repeated this process (connecting centers of faces repeatedly until there are zero faces) for all of the diagrams on page 117. Here are the results:
figure iteration faces faces column 4/ in diagram in polyhedron column 3 =================================================================== tetr | 0 | 4 | 4 | 1 | 1 | 1 | 4 | 4 | 2 | 0 | 4 | undef. ___________________________________________________________________ cube | 0 | 6 | 6 | 1 | 1 | 4 | 8 | 2 | 2 | 1 | 6 | 6 | 3 | 0 | 8 | undef. ___________________________________________________________________ octa | 0 | 8 | 8 | 1 | 1 | 6 | 6 | 1 | 2 | 1 | 8 | 8 | 3 | 0 | 6 | undef. ___________________________________________________________________ icosa | 0 | 20 | 20 | 1 | 1 | 9 | 12 | 4/3 | 2 | 10 | 20 | 2 | 3 | 3 | 12 | 4 | 4 | 1 | 20 | 20 | 5 | 0 | 12 | undef. ___________________________________________________________________ dodeca | 0 | 12 | 12 | 1 | 1 | 15 | 20 | 4/3 | 2 | 6 | 12 | 2 | 3 | 5 | 20 | 4 | 4 | 1 | 12 | 12 | 5 | 0 | 20 | undef.
It certainly seems to me that there are some nifty conclusions to be drawn from all this information, but snappy formulas elude me. I'm particularly leery of the data for the octahedron's first iteration. This first iteration looks just like the regular hexagon view of a cube. The problem is, it is the only figure in which the faces that I'm counting are not of the same type as the faces of the polyhedron. Since the faces are supposed to correspond to faces of a cube, I would expect them to be four-sided rather then three-sided. This, in addition to the fact that this is the only place in the data where column 4 does not increase with the iterations, makes me suspicious that I'm not correctly counting the sides in this figure.
 Keith_Adams@brown.edu
Keith_Adams@brown.edu