The wave fronts are very interesting. This chapter seems like an introduction to the large number of ideas that can be examined concerning these waves.
Especially interesting aspects are uncovered when we move things out of their dimensional constrains. Specifically, the waves of two dimensional objects in three space are quite interesting. The phenomenon of slicing a line's waves in three space to give either i) the wave fronts for a point in 2 space when sliced perpundicular to the line, or ii) the wave fronts for a line in 2 space when the slice contains the line, is very interesting and can be expanded dimensionally: the wave fronts of a plane in four dimensions can be sliced i) by a perpundicular hyperplane to give the three dimensional wave fronts of a line, or ii) containing the plane to give the three dimensioal wave fronts of the plane. The questions raised are i) what do you get when you make a slice parralel to the plane or line but not containing the plane or line? or ii) what do you get when you make a slice at an angle to the plane or line? or iii), can you slice the four dimensional wave fronts of the plane using two dimensional planes rather than hyperplanes to give two dimensional slices of a point's wave front? You surely can slice it to give wave fronts of a line in the plane, just remove one of the dimensions of the hyperplane that gave you the lines wave fronts in three dimensions.
Another interesting idea to explore, which is of vital importance in electricity and magnetism in physics, is the wave fronts of non-closed or non-infinite figures. Like a segment in the plane or three space, or a square in three space, or a closed cylinder (coke can) in three space. The options are endless and have surely been explored over the years. Under what category of mathematics is this type of work usually studied (topology, surface geometry)?
Once again this chapter gave insight to that interesting surface the Torus. So common growing up, not until this semester have I realized how interesting it really is. Because I was late getting last week's response in (and it deals extensively w/ the torus), I will include it here because it will probably not be read in last week's slot. Enjoy.
While reading chapter six, I did not feel that I had a good grasp on the Clifford torus until I examined the analogous situation for a Flatlander. In doing so I gained insight on many of the topics presented in this chapter: interelatedness of a cube and a sphere (whatever dimensional), rotation in general (including rotating cube, rotating hypercube (both the stereographic type shown in the book and the one in the film of the 2 cubes sliding in and out of each other), rotating 2 sphere, rotating 3 sphere), stereographic projections, and cylinders and their 2 dimensional counterparts.
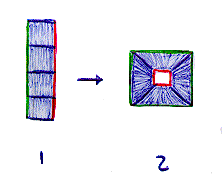
Working totally through analogy, here is the Flatlander's equivalent to the process presented in the book. Present a Flatlander with a "wingless" unfolded cube (fig. 1), and tell him (out of simplicity, I use "him") to connect the ends. Lacking the dimensions required to connect the ends without bending the squares, the Flatlander comes up with figure 2.

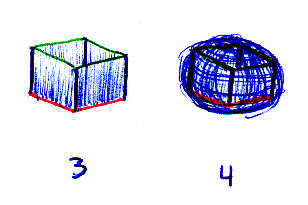
This interpretation maintains the squareness of the fold out (we see the 4 squares), but as Spacelanders we know that the intended connection would create a box with no top or bottom (fig. 3).
What is interesting about this outcome lies in the connection between figures 2 and 3: the Flatlander would actually create figure 2 when presented with the problem, but we would create the three dimensional figure 3, which would have the property that projecting it on the plane would give figure 2. Thus our figure 2 is both a 2D creation and a stereographic projection of the 3D cube.
Furthermore, the sections in the chapter describing the Clifford torus pointed out that the 16 vertices of the hypercube all resided on a hypersphere (3 sphere), and analogously, the 8 vertices of our box reside on a 2 sphere (fig. 4).
To make things cleaner, we can divide our "wingless" cube fold out into lots of thin slivers (fig. 1b), and then repeat our process with the Flatlander. When he connects the edges this time the outcome is a simple ring (fig. 2b).
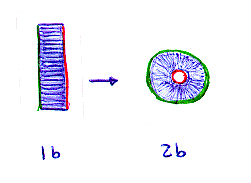
Notice how the Flatlander had to stretch the green spine while constricting the red spine (note connections w/ situation in fig. 2). We as Spacelanders know that the figure can be connected in three dimensions in such a way that nothing is stretched, and this construction gives a cylinder (fig. 3b).
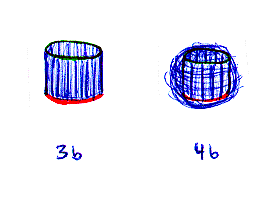
Once again we see how the Flatlander's construction is related to our 3D construction. Not only is the ring the Flatlander's construction, it is also the stereographic projection of our 3D cylinder.
Furthermore, as the division in the unfolded cube goes to infinity, the constructions become closer and closer to being a true ring and a true cylinder. Likewise, as every division is made, more vertices on the cylinder are created, each vertex lying on the two sphere. When a true cylinder is reached (effectively reached), we will have the situation presented in figure 4b, a cylinder inscribed in a 2 sphere (just like fig. 4). A phenomenon unique to the cylinder, however, is that every point on the green and red rims lies on the sphere, effectively producing the situation similar to pg 125 in B3D of a sphere with rings traced around it. Thus, when we project stereographically, we are projecting not just a cylinder, but a ringed sphere.
This ring is the Flatlander's Clifford torus.
The analogous situation of the above in three space was presented in B3D. If we were presented with a "wingless" fold out of a hypercube (fig. 4D-1), and told to connect the rims, the best thing we would be able to come up with would be figure 4D-2.
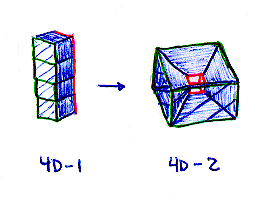
We lack the dimensions needed to connect the rims without bending the cubes; we would need at least four dimensions. We know that in four dimensions, the folded up figure would be a hypercube and would be inscribed in a hypersphere (the analogues to figures 3 and 4). The crucial point: the object we created out of figure 4D-1 in three space is the same thing as the stereographic projection of what a 4 dimensional being would create out of figure 4D-1. Figure 4D-2 is both a creation and a projection.
To make things cleaner, we can divide our "wingless" hypercube fold out into thin-many-sided-polygonal-prisms (a cylinder, fig 4D-1b) just as we divided the cube fold out into thin slivers (we have to divide the cube up in two ways, giving the 8x8 grid on pg 126, rather than just one way like in the cube because we have an extra dimension to deal with). Now when we connect the rims in three space, we get figure 4D-2b, which looks just like our normal torus.
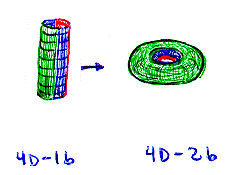
Notice how the green spine is stretched and the red spine is constricted. We can't imagine the construction, but a four dimensional being would be able to connect the rims of the cylinder so nothing stretched (analogue of fig 3b). Just like the rims of our earlier cylinder traced out two circles on the circumscribed 2 sphere, the "rims" of our "hyper-cylinder", which are two dimensional (the green and red faces on figure 4D-1b), will trace out two higher dimensional analogues to the circles before, a red and a green 2 sphere. Thus the stereographic projection from four space to three space of our hypersphere (or hyper-cylinder) with marked red and green "rings" will be the Clifford torus.
Thus, the torus that we created in three dimensions by "bending" figure 4D-1b is the same the Clifford torus (the stereographic projection of what a 4 dimensional being would create). They are the same thing but different at the same time, just as the rings for a Flatlander are the same thing but different. This was all very confusing until I traced out the dimensional analogue.
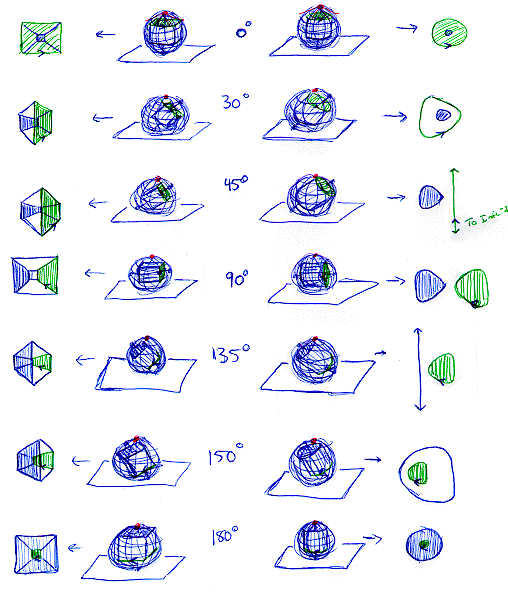
Just like the rotations in four dimensions of the stereographic projection of the hypercube and the Clifford torus look similar, the projections of the cube rotating and the "cylander" rotating are interelated and similar as well. Here we will give the light source on the sphere (red dot), the objects inscribed into their spheres, the angle of revolution, and the projection. Each object has a green face and a blue face. It is very effective to follow a single collumn all the way down. Notice two things specifically: i)how closely related the two projections are (and why they are different); ii)how related the two projections are to the projections of the rotating hypercube and 3 sphere. The blue arrows on the green curves are to better show the "orientation" aspect of the rotations, and how, to a Flatlander, the curves would seem to turn inside out (right handed becoming left handed).