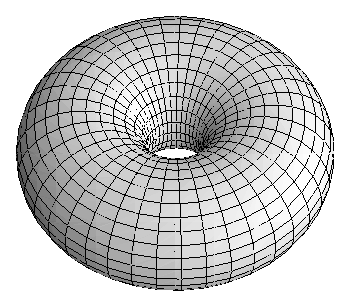

One of the most basic properties of the torus of revolution is the Spherical Two-Piece Property (STPP), which states that any sphere (or plane) divides the object into at most two pieces. Equivalently we may say that the intersection of the surface with any ball, or the complement of any ball, is connected.
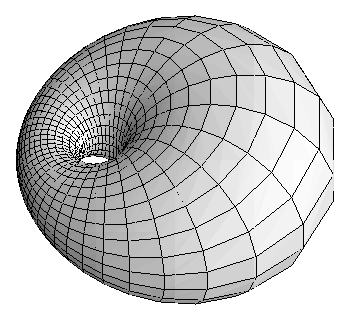
T his property is evidently shared by the inverted image of any STPP surface, and for the torus of revolution, this leads to the cyclides of Dupin, also characterized as the envelopes of families of spheres tangent to three fixed spheres.
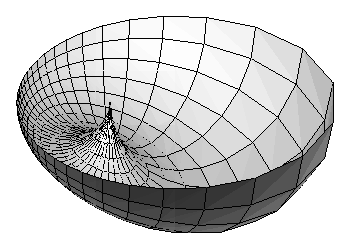
The parallel surfaces of a torus of revolution are also tori of revolution as long as they remain embeddings, and each of these will have the STPP. However, as the parallel surface develops singularities, the resulting objects will not have the ordinary STPP. It is easy to find a height function that has two local maxima, contradicting the usual STPP property that says in particular that no height function has more than one critical point.
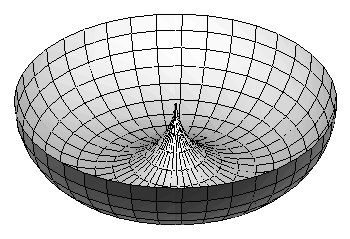
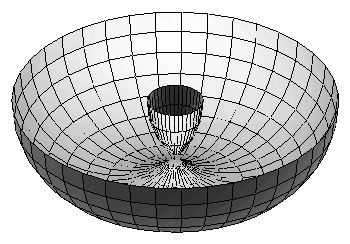
Is there a way to salvage a geometric interpretation of the STPP even for surfaces with conical singularities? Yes, it turns out that there is, using the concept of "intersection homology". In this theory two points will lie in the same connected component if there is a curve from one to the other not passing through any conical singularity. Under this definition the spindle torus will determine two components for the 0th intersection homology group, so it still might be that any point pair in a half space that bounds an arc (in the strict sence, following standards of singles behavior) will already bound in the half space.
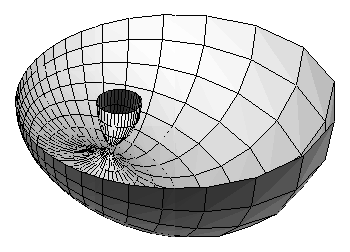
We illustrate this phenomenon with some key examples. The first is a torus of revolution and the second a cyclide of Dupin formed by inverting the torus in a sphere centered near the origin. We then show only the lower half of the torus to exhibit what happens when the radius of the offset object is greater than the radii of circles of curvature of a curve or surface. We obtain horn cyclides and spindle cyclides.
To see a beautiful color film of the deformation from the torus to the cyclide, select movie.
To see a beautiful color film of the deformation from the torus to the horn-torus to the horn-cyclide and back to the horn-torus select movie. Note that a portion of the surface has been removed to exose the interior structure.
To see still another beautiful color film of the deformation from the horn-torus to the spindle-torus to the spindle-cyclide and back to the spindle-torus and finally back to the original torus, select movie.