|
Convexity and Concavity
Text The second derivative of a function is the derivative of the first derivative.
 If f'(x) itself is differentiable, then its derivative with respect to x is denoted f''(x). If f''(x) > 0, then f'(x) is increasing and the shape of the graph is concave upward (or convex downward). If f''(x) < 0, then d'(x) is decreasing and the graph is concave downward (or convex upward). A point where the sign of the second derivative changes sign is called and inflection point.
If f'(x) itself is differentiable, then its derivative with respect to x is denoted f''(x). If f''(x) > 0, then f'(x) is increasing and the shape of the graph is concave upward (or convex downward). If f''(x) < 0, then d'(x) is decreasing and the graph is concave downward (or convex upward). A point where the sign of the second derivative changes sign is called and inflection point.

Demos
Convexity and Concavity

| 
|
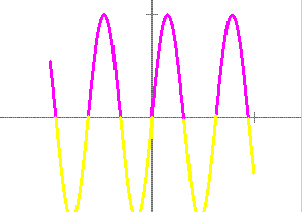
This demonstration is similar to 1.2.2 (critical points). As in 1.2.2, the function f(x) and its domain are defined in the control panel. This time, the graph of the function is colored magenta where it is concave downward and yellow where it is concave upward. 
|
Exercises 1. Using the demo, investigate the concavity of the following functions. For which intervals is the graph concave upward? For which intervals is it concave downward? For which intervals is there no concavity?:
- f(x) = x + 0.3
- f(x) = x2
- f(x) = x2 + x + 1
- f(x) = -3x2
- f(x) = x3 + 3x2 + 3x + 1
- f(x) = cos(x)
2. Describe the concavity of any function of the form f (x) = ax + b.
3. Now consider a function of the form f(x) = ax2 + bx + c. How do the values of a, b, and c affect the concavity of f(x)?
|