|
Area between Function Graphs
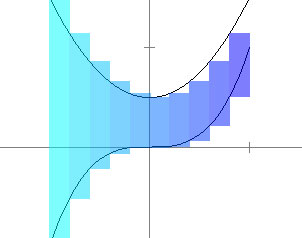
Text Consider two functions of one variable f(x) and g(x), and suppose we want to find the area of the region between the graphs of f(x) and g(x). Again, we can approximate the area by filling in the region with a sequence of rectangles.
 These rectangles can be obtained by using the rectangles in a Riemann sum of f(x) and subtracting the rectangles in a Riemann sum of g(x) that uses the same partition. Taking the limit of these partitions, we can write this in integral form as A = ∫ab f(x) dx - ∫ab g(x) dx, or equivalently, A = ∫ab (f-g)(x) dx.
These rectangles can be obtained by using the rectangles in a Riemann sum of f(x) and subtracting the rectangles in a Riemann sum of g(x) that uses the same partition. Taking the limit of these partitions, we can write this in integral form as A = ∫ab f(x) dx - ∫ab g(x) dx, or equivalently, A = ∫ab (f-g)(x) dx.

Demos
Area Between Function Graphs

| 
|
This demo shows how the area between function graphs can be approximated by rectangles. You can view either the right or the left rectangles by clicking the appropriate checkboxes. 
|
Exercises 1. Estimate the area between the function graphs for the example that the demo above begins with.
2. Estimate the area between the graphs f(x) = x2 and g(x) = 0. What integral does this represent?
3. How can you convert a problem involving area between function graphs into a problem involving the area under a single function graph?
|