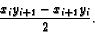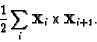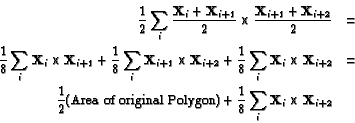The Problem
Convex Pentagons
Perimeter
What about perimeters for midpoint pentagons? For a regular pentagon, the midpoint polygon is another regular pentagon with sides equal to one-half the length of each diagonal. The ratio of the midpoint perimeter to the original is then the half the ratio of a side to a diagonal, i.e. one-half the reciprocal of the golden section, = 1/(2t), about .806 The same analysis shows that for a general convex pentagon, the perimeter of the midpoint polygon is half the sum of the lengths of the diagonals, and this definitely is not a constant.
Area
Now what about the areas of midpoint pentagons for convex pentagons? For a regular pentagon, the area of the midpoint pentagon divided by the area of the original figure is 1/(4t2). However for a pentagon close to a triangle, with two vertices close to one vertex on the bottom and two close to the other vertex on the bottom, the area of the midpoint figure is as close to 3/4 as we please. This appears to be the maximum ratio attainable for pentagons.

Demonstration 4. Area of midpoint pentagons
Note at this point, that for convex polygons with six or more sides, the ratio of the area of the midpoint pentagon to the area of the original is as close to 1 as we please. We can achieve this by placing the first two vertices near one vertex of a triangle, the next two near the second, and all the rest near the third. The ratio cannot be larger than 1 since the midpoint polygon lies inside the original convex polygon.