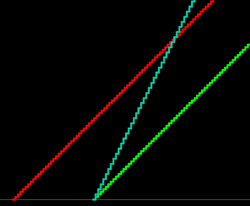

Twice As Old: Graph and Close-Up
At that point, I decided not to think about it any more because it looked like a good starter question for my calculus course in the fall. On the day of the first class, I gave the problem, without further elaboration, in the following form. "Last summer, my older daughter, Ann, observed that I was twice as old as her sister Mary Lynn, again. I was thirty when Mary Lynn was born. How old am I now, and for how many days was I twice as old as Ann?" I then sat back to watch. I was surprised and delighted with what occurred over the next few days.
My first-semester course in honors multivariable calculus was populated almost entirely by first-semester freshmen, all with a 5 on the Advanced Placement BC Calculus test, or the equivalent. The course is "paperless" in that all assignments are to be handed in over the web. There is a built-in time delay to avoid a competition to see who will be the first to solve the problem, thereby making it superfluous for anyone to continue. That was good, since the first person who answered, an hour after the end of class, solved the initial problem completely:
-------
Craig Desjardins at Tue Sep 05 18:13:28 EDT 2000
Since you were already 30 years old when Mary Lynn was born, you turned 31 before she turned 1, 32 before she turned 2, and so on including when she turned 30 in the midst of your 60th year. At that time you were twice as old as Mary Lynn. Then, as time passed, you turned 61, she turned 31, and you turned 62 just as before. At this time, when you are 62 and she 31, you are once again twice her age. You are 62. Since Ann is older, you have already been twice her age, twice for that matter (unless you have the same birthday, a case in which the answer to this question is only too obvious). The number of days that you were twice her age the first time is the number of days from her birthday and your birthday chronologically. The second time it was the number of days from your birthday to her birthday, also chronologically. Since this comprises an entire year, the number of days during which you were twice Ann's age is either 365 or 366, depending on leap year. -------
Later that evening, another student, Josh Butler, offered a geometric illustration:
If you graph the days of a year as equal-length arcs on a circle, your birthday and her birthday will be two arcs. Shading each day/arc from her birthday to your birthday the first time you were twice her age, then shading from your birthday to her birthday the second time you were twice her age, will effectively shade the entire circle exactly once. Thus, depending on whether a leap-day fell while you were twice her age you were twice her age for either 365 or 366 days.
---------
The surprising thing is that the question generated so many other general questions over the course of the next several days. The first observation is that the analysis above shows that it does not make any difference what the actual birthdates are, as long as those birtdays are different. If my daughter had been born on my birthday, I still would have been exactly twice as old for a calendar year, but I would not have been twice as old "again", i.e. on two separate intervals. In particular, the analysis shows that there is nothing special about the number 30 when it comes to being twice as old. The total number of days I was twice as old as Ann is a full year, independently of my age when she was born (assuming that she is not just born ahead of her sister in a multiple birth, in which case the full year would not be up at the time of the observation.)


The thing that makes the problem interesting in a calculus course is the relationship with the Intermediate Value Property. In our classes we stress the fact that if one continuous function starts out below another and surpasses it as some future time, then for some intermediate point, the two functions must be equal. (Actually we stress this theorem in a sligthly different form but the concepts are equivalent, for continuous functions in any case.)
In the case at hand, the problem is of the sort "A train leaves Philadelphia 30 minutes after another has left on a parallel track, but the second train goes twice as fast. Where do the trains meet?"
For linear functions, the answer is that the two trains arrive at the same point exactly once, and just for an instant.
Here, however, where age is measured in full years, changing only at birthdays, we have a pair of step functions, clearly discontinuous. Why should they have any overlaps at all, and what will the nature of those overlaps be?
Students are familiar with a number on instances where discontinuous functions do not have to meet in order to cross, even in the case where both are increasing functions. Sports scores provide the most accessible examples. If one American football team is ahead at the half but the other wins, then there did not have to be any time when the scores were the same, since the lead could change with a touchdown. European football, or soccer, has a different scoring structure, and there has to be a time when both scores are the same if one team is to overtake another. Basketball is of the first type and ice or field hockey is of the second. Baseball, with its very specific and sometimes arcane rules, is a special case. Can the score of a game ever go up instantaneously by two runs? That does not happen if there is a home run with one person on base since the run is scored only when a runner crosses home plate, so two runs are scored in quick succession, but not at the same time. There are other more obscure and somewhat contrived scenarios that cause greater difficulties, although whether or not two or more runs appear simultaneously will not affect who wins the game so the problem is of "academic interest".
We can distinguish two kind of overlap intervals, where two functions have the same value. If f(t) = g(t) for an entire interval a < t < b, then we say that the interval is a crossing interval if f(t) < g(t) for a - h< t < a and f(t) > g(t) for b < t < b+h, for some positive h, in which case f is said to overtake g, or the opposite happens, inwhich case g overtakes f over the interval. If f and g are both step functions that can jump exactly one unit, then the Intermediate Value theorem holds, namely the result that if one overtakes the other, there must be a crossing interval sometime in between. Moreover, there must be an odd number of crossing intervals under these circumstances, since only at such intervals can the lead change hands, and it must end up at a different place than it started.
Although the function g(t) = "my age plus 30" jumps by one unit every time I have a birthday, the function f(t) = "twice my daughter's age" jumps by two units every birthday. However the analysis above indicates that f and g can be equal on two separate intervals. By now, f(t) > g(t) and it will stay that way. So which of the intervals is a crossing interval? Must there be an odd number of crossing intervals? Where did f overtake g? One surprise is that neither of the intervals where f was equal to g was a crossing invertal, and the overtaking happened instantaneously at my daughter's birthday that occurred between the two intervals when my age was twice hers. This becomes clear if we graph the two functions on the same diagram. Twice her age starts out below, then catches up at the first coincidence interval, then drops below then jumps above at one point, then drops back for another interval, then goes ahead for good.

Abbott: You're 40 years old, and you're in love with a little girl, say 10 years old. You're four times as old as that girl. You couldn't marry that girl, could you?
Costello: No.
Abbott: So you wait 5 years. Now the little girl is 15, and you're 45. You're only three times as old as that girl. So you wait 15 years more. Now the little girl is 30, and you're 60. You're only twice as old as that little girl.
Costello: She's catching up?
Abbott: Here's the question. How long do you have to wait before you and that little girl are the same age?
Costello: What kind of question is that? That's ridiculous. If I keep waiting for that girl, she'll pass me up. She'll wind up older than I am. Then she'll have to wait for me!
(I am indebted to Ivars Peterson for providing the reference to this dialogue in his weekly online column for the MAA.)
------------------
It appears that 30 years of separation provides a good basis for the mathematical joke above, but is there something special about 30? And how many times was I n times as old as Mary Lynn, where n is an integer? This refined question was answered by Ryan Roth in his posting two days later:
Ryan Roth at Thu Sep 07 19:29:48 EDT 2000 There are quite a few times when Professor Banchoff was n times older than his daughter. (here n is an integer.) These values occur at n=2,2,3,4,6,7,11,16,31,32 n=2 is the only to occur twice.
---------------
Ryan then went on to write a Basic program to figure how many distinct numbers n would show up for various starting ages. In all of the cases he checked, the answer came out to be even. However subsequent investigation showed that 15 (an early age for parenting but still possible) yielded 1,2,3,4,5,8,15, and 16. He asked the conditions for this number to be even. That question was answered only after the general situation was analyzed.
The most extended investigation took place as a dialogue between Gregory Balthazar, and Steve Canon, a senior who acted as an assistant in the course. The interchange is reproduced here in its entirety.
--------------
Gregory Baltazar at Thu Sep 07 23:33:16 EDT 2000 If n is an integer, then n can equal 2, 3, 4, 6, 7, 11, 16, 31, 32 times as old as ML [ Expatiate ]
Stephen Canon at Fri Sep 08 14:02:53 EDT 2000 What if Professor Banchoff wasn't 30 when she was born? If he was 31 years old, then which n work? If he was 32? 33? etc.? Can you find any interesting patterns? Can you prove them?
Gregory Baltazar at Sat Sep 09 02:28:32 EDT 2000 Well, let's say that professor Banchoff's age is represented by the letter X. Then 1 + any divisor of X is an n.
Proof: X=professor Banchoff's age when ML was born Y=years that have elapsed since the birth
(X+Y)/Y = n So, if you want n=2, let X=Y (X must be divisible by one) *therefore n can always be 2 if you want n=3, let X=2Y (X must be divisible by two) if you want n=35, let X=34Y (X must be divisible by 34) and so on . . .
N.B. I don't know why I'm writing this at 2 in the morning. For reasons beyond my control, I've become nocturnal.
Stephen Canon at Sat Sep 09 19:07:56 EDT 2000 Yes, 1 plus any divisor of X is such an n, but there are more n's besides. Can you find some? Can you describe all of the n's? Keep working!
Gregory Baltazar at Sat Sep 09 23:17:02 EDT 2000 Are you referring to the intance in the "twice as old" problem where it was possible for Professor Banchoff to be 30 years older than ML as well as 31 years older than ML?
Stephen Canon at Sun Sep 10 00:20:10 EDT 2000 It's related, but no. For example, if X=11, then n=4 is a solution, even though 3 doesn't divide 11. (Specifically, it happens when prof. B is 16).
Gregory Baltazar at Mon Sep 11 12:38:09 EDT 2000 Ok then, The set of all n consists of 1+the divisors of X and 1+the divisors of X+1.
Stephen Canon at Mon Sep 11 22:55:58 EDT 2000 exactly. good work. You've shown that any divisor of X or (X+1) will yeild an n. Now can you prove that every n is of the form (1+d), where d is a divisor of X or (X+1)?
Gregory Baltazar at Tue Sep 12 09:05:39 EDT 2000 Same proof for X+1 as in the proof for X above. Just substitute X+1 in for X.
Stephen Canon at Sun Sep 17 14:23:42 EDT 2000 Well, that's not what I asked. You proved that every n of the form (d+1) where d divides X or X+1 works. But you are yet to prove that these are the only n's that will work. i.e. you haven't yet proved that there can't be some n that isn't of the form (d+1). Do you understand?
Gregory Baltazar at Mon Sep 18 18:52:53 EDT 2000 Well, all n are of the form: n=(X+Y)/(Y), where X is the professor's age when ML is zero years old and Y is the number of years that have elapsed since ML's birth. This simplifies to n= X/Y + 1 Now n doesn't have to be of the form d+1 Professor Banchoff could be 2.5 times as old, if he was 30 at her birth and he is now 50. But, if you want n to be an integer, then n-1 is also an integer. This means that the term X/Y is an integer or to put it in technical terms: X/Y=k, where k is a nonnegative integer. (it wouldn't make sense for Prof. B. to be (-2+1) times as old as ML for example) Then X=kY, which means that X is a multiple of Y or Y is a divisor of X. Since X/(X/Y)=Y, (X/Y) must also be a divisor of X. So all n are of the form (d + 1) where d is a divisor of X.
Stephen Canon at Tue Sep 19 13:55:47 EDT 2000 well done. Sorry to pester you so much, but we often like to write things down really precisely in mathematics, just to make sure that we aren't missing something.
----------
Perhaps the most succinct treatment of the topic was by Ju Dee Ang, nearly a week after the problem was first introduced:
Ju Dee Ang at Mon Sep 11 00:31:23 EDT 2000 I would assume that you are referring to integer values of n (or perhaps not?). Let m be Mary Lynn's age at any time, in which case n=(30+m)/m or (31+m)/m. So n could only be an integer if m is a factor of 30 or 31. For Mary Lynn, the possible values of m when n would be an integer would be when she is 1, 2, 3, 5, 6, 10, 15, 30 or 31 years old, when n would be 31, 16, 11, 7, 6, 4, 3 or 2 (twice). ----
Ju Dee Ang at Tue Sep 12 00:55:27 EDT 2000 Yes, and I forgot about n=32 for Mary Lynn, given by(31+1)/1.
Following the lead given by Gregory Baltazar and Ju Dee Ang, we can answer Ryan Roth's question. The number of distinct n that will appear in the "n times as old" problem is the number of divisors of m plus the number of divisors of m + 1, minus 1, where m is the age of the father at the birth of the daughter. Thus that number will be odd unless either m or m+1 is a square.
It was a very complete answer to a problem that began with a chanceobservation, a great way to get a class involved in developing amathematical idea and seeing where it goes. Now I just have to findanother equally stimulating problem for my next class.

Addendum, Concerning Horses
According to The University of Georgia College of Agriculture and Environmental Sciences, Cooperative Extension Services, a stallion can sire a filly who is born while he is officially still one year old. He will then turn two years old on January 1, the same day his daughter turns one. He will be twice as old as she is for exactly one year, and there will never be another time when he is an integer times as old as she is. This is the absolute minimum number of times that a father can be an integer number of times older than his daughter.
For human beings, the minimum number of times is two, which occurs when the father and daughter share the same birthday and the father's age is a prime number when his daughter is born.
Additional Addendum: Following my J. Sutherland Frame lectureincluding this topic at the MAA MathFest, I received a note fromJerrold Grossman from Oakland University pointing out a similarobservation made by the young Dan Kleitman, as reported in the Journalof Discrete Mathematics 257 (2002) 193-224: "Kleitman's brother Davidtells us when he realized that his brother would probably become amathematician. 'When Danny was 3 years old, we were playing in asandbox. The parent of another child in the park asked us how old wewere. I said I was 6, and my little brother was 3. "You are twice asold as he is," the parent replied. Danny apparently though aboutthat, because he said, "You know, after my birthday next month, thatwon't be true anymore. It will never be true again."'" Grossmanobserves, "Aha! He is right, but it WAS true 22 months previous tothat, when David was 4 and Dan was true. Maybe you can work that intoyour article on birthday multiples." Thank you, Jerry.