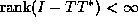The main result of the paper is that a system of invariant subspaces
of a (completely non-unitary) Hilbert space contraction T with finite defects
(
,
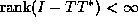) is an unconditional basis (Riesz basis) if and only if
it is uniformly minimal.
Results of such type are quite well known: for a system of eigenspaces of a contraction with defects 1-1 it is simply the famous Carleson interpolation theorem. For general invariant subspaces of operators with defects 1-1 such theorem was proved by V. I. Vasyunin. Then partial results for the case of finite defects were obtained by the author.
The present paper solves the problem completely.