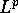 .
.
The main goal of the paper is to demonstrate the abilities of a new (old?) powerful technique in the harmonic analysis. This technique --- the method of Bellman function was ``borrowed'' from the applied mathematics, more precisely from the control theory. It is interesting to note that although usually the applied mathematics gets ideas from the ``pure'', here we have an oppposite example.
The idea to apply the Bellman function method to the problems in
harmonic analysis is also nothing new. D. Burhgolder
(see [1]) applied a variation of the method (without mentioning
the term ``Bellman function'') to different problems in harmonic
analysis, e.g. finding the sharp unconditional basis constant for the
Haar system in 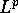 .
.
We discovered the method when (successfully) trying to generalize the result of [3]
about weighted norm inequalities with matrix weights to the case
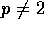 . Initially the problem looked extremely difficult, and we could not obtain this result using any other known
method. (Recently A. Volber found an alternative approach
allowint to solve the same problem. Unlike ours, his approach uses a
lot from the classical theory of singular integral operators.) And the Bellman function was the tool that allowed us to crack
the problem and finally to solve it completely. So one of the main
results of the paper is a generalization of the Muckenhoupt
. Initially the problem looked extremely difficult, and we could not obtain this result using any other known
method. (Recently A. Volber found an alternative approach
allowint to solve the same problem. Unlike ours, his approach uses a
lot from the classical theory of singular integral operators.) And the Bellman function was the tool that allowed us to crack
the problem and finally to solve it completely. So one of the main
results of the paper is a generalization of the Muckenhoupt 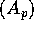 condition (
condition (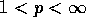 ) to the case of matrix weights and the corresponding theorem
about weighted norm inequalities.
) to the case of matrix weights and the corresponding theorem
about weighted norm inequalities.
However, as we can clearly see now, the paper contains more than just the proof of the above theorem. Let us describe what we have done in more details.
After [3] appeared it was clear (at least for the authors, as
well as for A. Volberg)
what should be the right matrix analogue of the Muckenhoupt 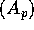 condition --- simply the uniform boundedness of the corresponding
averaging operators, although the elegant form with dual norms
appeared only during the work on the paper.
condition --- simply the uniform boundedness of the corresponding
averaging operators, although the elegant form with dual norms
appeared only during the work on the paper.
Thus the proof that this matrix 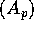 condition (which is called
condition (which is called
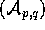 ,
, 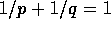 in the text) is necessary for
the boundedness of the Hilbert Transform is quite straightforward, and
the hard part is the sufficiency. Following [3] we split the
proof into 2 parts: finding an appropriate basis, and showing that the
matrix of the operator in this basis is ``good'' and so is bounded in
the corresponding coefficient space.
in the text) is necessary for
the boundedness of the Hilbert Transform is quite straightforward, and
the hard part is the sufficiency. Following [3] we split the
proof into 2 parts: finding an appropriate basis, and showing that the
matrix of the operator in this basis is ``good'' and so is bounded in
the corresponding coefficient space.
The choice of the basis was clear for us: like in [3] it is the Haar system. The reader might think that smooth wavelets would be a better choice and that we use the Haar system only because we are not very comfortable with wavelets. But it is not the case. Indeed, a standard way to prove that the wavelets form an unconditional basis uses the boundedness of Calderon--Zygmund singular integral operators. By that is exactly what we need to prove!
On the other hand, the martingale structure of the Haar system is very essential for us: it allows to apply the Bellman function approach to show that the Haar system forms a strong unconditional basis, see formal definition in the paper. The coefficient space turns out to be the same Triebel--Lizorkin space as for the scalar case.
This is the hardest part of the proof. The proof of the boundedness of the matrix is much simpler. It uses an elegant trick, which we think is interesting by itself. We think it is the right way to deal with operators in Triebel--Lizorkin spaces.
When working with singular integral operators, the Haar system has one disadvantage comparing to wavelets: the matrix of the operator has ``singularities'' when the discontinuities of two Haar functions are close to each other. However, if we consider random dyadic lattices and the corresponding Haar systems, the probability of a ``bad'' pair is small, so taking an average over all dyadic lattices we were able to get rid of the above singularities. An informal conclusion from that: if you can do something with wavelets, you can do the same with the Haar system (may be you will need averaging).
Finally, as a bonus we were able to obtain some new results
about bases of wavelets. Using the result about the Haar system we
proved that any wavelet system (satisfying some very mild assumptions,
that
all classical wavelets satisfy) forms a strong unconditional basis in the
weighted space 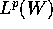 with matrix
with matrix 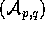 weight W. We were also
able to describe the coefficient space: it was the same
Triebel--Lizorkin space as in the case of the Haar system.
weight W. We were also
able to describe the coefficient space: it was the same
Triebel--Lizorkin space as in the case of the Haar system.
In scalar weighted case the result about bases of wavelets is due to Lemarié [6] (for compactly supported wavelets); but the description of the coefficient space was not known.
Also, for the completeness of the theory we included the result about boundedness of the maximal operator (see Appendix 2).
The paper is big --- over one hundred pages, but the reader should not get afraid. First of all, it is completely self-contained. We even included a ``chapter from a functional analysis textbook'' about strong unconditional bases.
Second, a lot of pages is devoted to how one could find a Bellman
function. To get a perfectly correct formal proof we could simply
present a function, and say that it satisfies such and such properties
(some versions of convexity) --- in the age of computers it should not
be a problem to verify that properties. An extreme example of such approach is an
elementary proof for the scalar 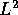 case presented in [4].
But we tried to show all motivations, to show how we
found (and therefore how the reader can find) the Bellman function. So
we included almost all computation. We think it will help the reader
a lot
to master the machinery.
case presented in [4].
But we tried to show all motivations, to show how we
found (and therefore how the reader can find) the Bellman function. So
we included almost all computation. We think it will help the reader
a lot
to master the machinery.