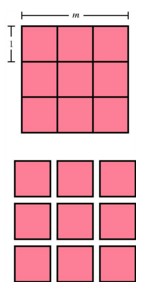
A square of side length msubdivided into m2 unit squares.

Patterns that arise in the formulas of plane geometry often correspond to patterns in the formulas of solid geometry, and they may suggest analogous relationships in higher dimensions. One of the simplest of these patterns arises when we measure the length or area or volume of the basic building blocks in any dimension -- namely a segment in a line, a square in a plane, and a cube in space. In the line, a segment has length an if we can cover it exactly by m segments of unit length. Similarly in two dimensions, square with side length m can be filled exactly with m² unit squares. And in three dimensions, a cube having side length m can be filled exactly with m³ unit cubes. The pattern is in the exponents: in dimension n, the volume of an n-cube having sides of length m is n², so a four-dimensional cube having sides of length m would be filled with exactly m⁴ unit four-dimensional cubes.

A cube of side length msubdivided into m3 unit cubes.

But is there a geometric configuration that corresponds to this expression m⁴? It would have to be four-dimensional, and indeed it does exist in four-dimensional space, if we interpret the word exist in a different way than in ordinary speech. When we speak informally, about a square, we think of chalkboard sketches, or much more exact renditions on an architect's table or on a computer-aided drafting device. Yet the formal geometric theorems pertaining to a square are about none of these physical representations, but about the abstract idea of the square, more perfect than anything we can construct. As the followers of Plato might put it, the ideal square exists only in the mind of God. It is such an ideal square that has side length exactly in covered precisely by m² unit squares. Similarly the volume formulas refer to perfect cubes, not to the physical representations we see around us. So it is also that the four-dimensional version of this algebraic expression corresponds to an ideal object, a hypercube having side length, existing in the mind of that same God, and filled with m⁴ perfect unit hypercubes. The difference is that we are able to construct in space a model of the m⁴ solid cubes, while it is not possible for us to build a similar model of m⁴ hypercubes.

			Volume Patterns for Pyramids
			Table of Contents
			Introduction