 |
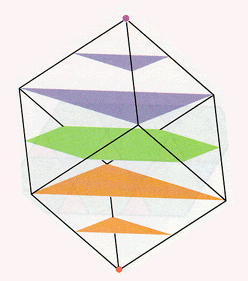 |
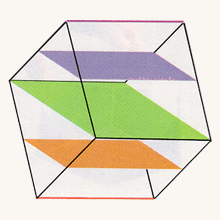
Slicing the cube edge first (left); slicing the cube vertex first, perpendicular to the long diagonal (right).
Coming back to the ordinary cube, we can ask about other ways that it can pass through the water's surface. If it is hung from the center of an edge, then the opposite edge is the first part to get wet. As the cube sinks farther, the slice becomes a rectangle having one pair of sides of length equal to the length of the first edge and another pair of sides of very small length at first. This pair of sides grows until it surpasses the first pair, reaching a maximum length nearly one and a half times that of the original length. Then the length of that pair of sides shrinks back to zero, as the slice becomes a single edge just as the entire cube submerges.
The most difficult slicing sequence to visualize occurs when when we suspend the cube from one of its vertices. The lowest vertex gets wet first and then expands to form a small triangle as the water level meets three of the six square sides. When the cube is almost fully submerged, we see another triangular slice, which shrinks down to a single point, the point of suspension.
| |||
Slicing the cube edge first (left); slicing the cube vertex first, perpendicular to the long diagonal (right). |
You might want to try to imagine what we get in the middle. When the water level has covered exactly one half of the cube, what is the form of the slice? Many people are surprised at the answer. Halfway through the cube, perpendicular to the long diagonal, we get a perfect regular hexagon, with all six sides of equal length and all angles equal. The answer is reasonable. After all, halfway through we expect to hit something, and there isn't any reason to prefer the upper three faces over the lower three, so we should hit all six faces, and in the same way. Therefore just by reasons of symmetry we should expect to see a hexagon. Such an abstract argument is perfectly convincing for many people, but quite a few others prefer to see an illustration. For example, we could fill a transparent cube with colored liquid and hold it up in various positions. Or we could instruct a modern graphics computer to show us the slices in any given direction.
Movie of the slicing of a three-dimensional cube.
The appearance of the hexagon as the middle slice of a cube tells us something about the symmetry of the cube. The cube has four long diagonals that pass through its center, and there is a halfway hexagon perpendicular to each of them. The midpoint of each edge will be a corner of two of these hexagons.
Patterns of hexagons and triangles and squares are quite important in the mathematical subject called tiling. Consider what happens if we stack a large number of cubes together to form a large cube. If we slice the large cube by a flat plane, then in each of the cubes hit by the plane, we get a slice in the shape of a polygon. All of these separate pieces will fit together to cover a portion of the slicing plane. If this plane is parallel to one of the faces of the large cube, then all polygonal slices will be squares, and these squares fit together to form a "tiling" pattern in the plane. This is an example of a regular tiling, where all polygons have the same shape. Now consider a slicing plane perpendicular to a long diagonal of the large cube. If such a slice goes through a vertex of a cube, then all of the slices will be equilateral triangles and again we have a regular tiling. If the slicing plane is moved parallel to itself until it goes through the center of a cube, then some of the slices will be regular hexagons, while the adjacent slices will be equilateral triangles. This pattern is a "semi-regular" tiling of the plane, whose polygonal slices are all regular but have varying numbers of sides. Slices in other directions may give tilings of the plane by irregular polygonal figures. The patterns that arise from slicing in different directions are similar to patterns found in crystallography.
| ||
The pattern of triangles and hexagons in a slice through a collection of cubes. |
| Slicing the Hypercube | ||
| Table of Contents | ||
| Slicing Basic Three-Dimensional Shapes |