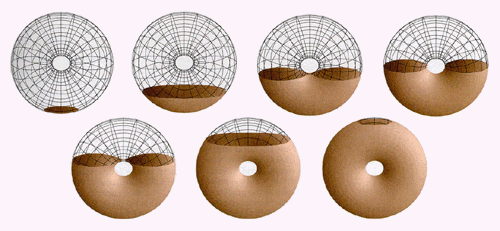
 |
Slicing the torus held vertically, as a doughnut.
Slicing techniques are also a tool for investigating smooth surfaces other than spheres and islands. One shape that shows up often enough to merit special consideration is the ring-shaped figure known as a torus. We see this shape in the surface of a doughnut or a bagel, and the surface of a life preserver or a Life Saver candy. By the end of this book, we will encounter the torus in the study of configuration spaces in physics and in the generalizations of perspective to higher dimensions, but for now we wish to consider its slice history as a geometric object in ordinary space.
One of the easiest ways to obtain a torus is to generate a surface of revolution. We think of a circle as drawn on a square in a vertical plane, and we attach one vertical edge of the square by hinges to a pole called the axis. As the square rotates around the pole, the moving circle traces out a torus. We can use the same method to generate a sphere, by drawing in the square a semicircle and attaching both endpoints to the axis.
The sphere is called "two-dimensional" because we can identify any point (other than the north and south poles) uniquely by giving two numbers, the latitude showing the position of the point on its semicircle, and the longitude indicating how far the semicircle has been rotated. A torus is a two-dimensional surface in the same sense. We can give latitude and longitude coordinates for each point on the torus, where now the latitude shows the position anywhere on the vertical circle. Each point on the torus of revolution is specified uniquely by two coordinates. There are no "special points" like the north and south poles on the sphere.
For the slice history of a torus, we think of what happens as we dunk a doughnut in a cup of coffee. The doughnut first meets the surface of the coffee at a single point. If A Square were floating on the surface as the doughnut came through, he would observe the point expand into a small disc, and he might think that he was being visited by a sphere or that he was watching the slice history of an island with a single peak. But something quite different occurs, as two indentations appear on opposite sides of the contour, then come together on the inside as the contour breaks apart into two ovals. Halfway through the surface of the coffee, the doughnut appears as two perfect circles, side by side. The second half of the story is the reverse of the first: two ovals come together and form a single curve, which shrinks to a point as the doughnut disappears below the surface.
| ||
Slicing the torus held vertically, as a doughnut. |
There are four critical levels in this slice history, the two points at the top and bottom, and two "figure eights" where pairs of curves break apart or come together. This slice history is quite different from that of a sphere, with its two critical levels each consisting of a single point. Critical point theory gives essential information about the shape of a surface.
Slicing a sphere from different viewpoints gives us no new information since we always get the same sequence of shapes. For a torus, however, different positions tell us quite a bit about the structure of the object. Instead of dunking a torus-doughnut, consider the usual way of slicing a torus-bagel. We set the torus on a plane so that it rests on a circle of latitude. As we slice by horizonal planes, the first slice is a single circle where the bagel rests on the plate. We then get a flat ring-shaped slice with two circular boundaries, each centered at the point where the slicing plane intersects the axis. One circle expands while the other shrinks until we reach the halfway point, after which time the two circles come back together at a top circle. There are only two critical levels, the first and the last circles.
| ||
Slicing the torus held horizontally, as a bagel. |
If we tilt the bagel slightly, we get a different phenomenon. Now the slices start with a single point, which grows to be a disc from which two "pseudopods" emerge. These come together at a critical level to form a curve with a loop, similar to the level through the mountain pass in the slice history of the tilted Crater Lake in the previous section. The slice curve then breaks apart to form two closed curves, one inside the other. Halfway through we get a pair of symmetrical ovals, and then the process reverses itself, as the inner oval becomes attached to the outer, then forms a single curve which shrinks down to a point and disappears.
| ||
Slicing the tilted torus to reveal two interlocked circles. |
You can watch the torus being filled in at Movies of the Torus Triptych.
If we continue to tilt the bagel toward a vertical position, its slice history will become the same as that of the doughnut. Somewhere in between there has to be a particularly interesting position where a changeover occurs. At this exceptional position, instead of observing four different critical levels, we see only three. We get a single point at the top and a single point at the bottom as before, but the halfway slice consists of a curve that comes together at two different points, forming two intersecting circles! Each of them goes once around the axis and hits each circle of latitude and each circle of longitude exactly once. The torus is so symmetrical that through every one of its points there pass two of these circles in addition to the circles of latitude and longitude. This remarkable family of circles will appear in an extremely significant way in a later chapter, in the study of orbit spaces of systems of pendulums.
| Table of Contents | ||
| Contour Lines and Contour Surfaces |