 |
Construction of a three-simplex by lifting the center of a two simplex.
What about polytopes made out of tetrahedra? In the previous chapter, we discussed a method of building one such object, the four-dimensional simplex, or pentatope. This object is the simplest polytope in four-space, analogous to the triangle in the plane and the tetrahedron in three-space. To construct a four-simplex, start with a segment in the plane, and draw the line perpendicular to it through its midpoint. Any point on this line is equidistant from the two endpoints. If we go out far enough, the distance to the endpoints is equal to the length of the segment and we have a regular triangle, also called a two-simplex.
| ||
Construction of a three-simplex by lifting the center of a two simplex. |
Now draw the line in space perpendicular to the triangle through its center. Although the Flatlanders cannot appreciate this construction, we know that any point on this line is equidistant from the vertices of the triangle, so if we go out just far enough, we find a vertex with distance equal to the side lengths of the triangle. This produces three new equilateral triangles congruent to the original triangle, and we have constructed a regular tetrahedron, or three-simplex.
In a similar way, we may consider a line in four-dimensional space perpendicular to the tetrahedron through its midpoint. We in three-space cannot see this line, but we know that any point on it is equidistant from all vertices of the tetrahedron. If we go out along this line just far enough, we find a point with distance equal to the lengths of the sides of the original tetrahedron. In this way we obtain four new tetrahedra, each congruent to the original tetrahedron, forming a regular four-simplex in four-dimensional space.
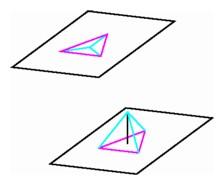
We do not have physical access to that fourth direction, so we cannot actually construct the four-simplex. Nevertheless, using the techniques of the previous chapter, we can still draw pictures of its shadows in the plane or in three-space. When we draw a tetrahedron in the plane, we choose four points and connect all possible pairs. We get two different sorts of views, depending on whether or not one vertex is situated inside the triangle formed by the other three. Similarly there are two different sorts of projections of a pentatope into three-space, depending on whether or not one vertex is contained inside the tetrahedron formed by the other four. The first example on this page has four vertices on the outside and one inside, six edges outside and four inside, and four triangles outside and six inside. In the second example, all vertices are outside, all edges but one are outside, and there are six triangles outside and four inside. There is a major difference between the two representations. In the first it is possible to put in all ten triangles without having any one intersect any other, while in the second the three vertical triangles and their common edge all intersect the horizontal triangle.
| |||
Symmetric projection of a four-simplex into three-space. Displacing the center point perpendicularly into four-space makes all 10 edges equal in length (left). Two projections of the four-simplex into three-space, with inner triangles filled in (right). |
Either projection of the four-simplex shows three tetrahedra at each edge, just as there are three cubes at each edge of a hypercube. Analogous to the configuration of three cubes around a line, we may arrange three tetrahedra around an edge in three-space, with room to spare.
To see how many regular polyhedra can be placed around an edge in three-space, we sum the dihedral angles of each polyhedron, the angles between the two planar faces of the polyhedron that come together at the edge. In the case of the tetrahedron, we can think of the dihedral angle as a planar angle by holding the tetrahedron with one edge vertical and the opposite edge horizontal, and then slicing through the middle to get an isosceles triangle. The angle of this triangle that lies on the vertical edge will be the dihedral angle at the edge. It is larger than the angle of an equilateral triangle, so six tetrahedra cannot fit around an edge.
| |||
Three tetrahedra around an edge in three-space (left); the dihedral angle at the center of one edge of a three-simplex (right). |
| The Hypercube Dual or Sixteen-Cell | ||
| Table of Contents | ||
| The Search for Regular Polytopes |