The Self-Dual 24-Cell
|
|
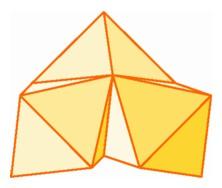
Three octahedra around an edge in three-space. |
The dihedral angle of the octahedron is larger than that of the cube and smaller than that of the dodecahedron, and so we can fit three octahedra around an edge but not four. It follows that there is a possible regular polytope in four-space with octahedral faces. Such an object does exist. Having 24 octahedral cells, it is called the 24-cell (see illustration on the following page). Around each vertex of such an object there will be six octahedra. Therefore the cells of the dual polytope each have six vertices, and these dual cells too are regular octahedra. The dual of the 24-cell is another 24-cell, so this polytope is self-dual. The surprise then is that there are more regular objects in four-space than there are in three-space, even though in higher dimensions we only find the three basic types.
According to Abbott, contemplation of higher dimensions leads to
humility. That certainly was true for the many mathematicians in
the 1880s who vied for the honor of being the first to find all
of the four-dimensional regular polytopes. We have proven that
there can be at most six regular polytopes in four-space, and so
did they. Which of them deserved the credit for the discovery?
The entire competition turned out to be meaningless when it
became known that the result had been proven more than 30 vears
earlier by the Swiss mathematician Ludwig Schlafli, in a long
work on higher-dimensional geometry which contained not one
picture!
|
|
Projection of the 24-cell into three-space. Highlighted are
the differently shaped projections of two octahedra. |