 |
 |
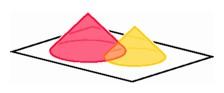
Left: Cones of light from bulbs suspended above a stage determine circle patterns on the floor. Right: The coordinates for the center and radius for each disc of light indicate whether or not the disc will remain completely within the stage area.
Consider a highly simplified example that leads to a fairly intricate space of geometric objects. The lighting director of a local theater has to arrange a set of lights over the stage so that they illuminate certain parts of the floor at certain times. Sometimes the size of a spot needs to change during the course of a performance. Sometimes one colored circle of light must be contained in another. How can she keep track of all the circles of light, and how can she design her lighting directions so that her assistants can carry them out?
The lights all have the same form. A single bulb is suspended from a wire hanging from the ceiling, and a conical shade directs the light out in a beam, which meets the floor in a disc of light. The sides of the shade come down at such an angle that the radius of the disc is equal to the height of the bulb above the floor. Thus the lighting director can specify the radius of the disc by specifying the height of the bulb above the floor, a feature that makes it easy for the director to specify the location of any light. She can always indicate the position of the center of the disc by noting the coordinates used by the director of the play to give her instructions, and for a complete specification, she adds a third coordinate giving the radius, or the height. The collection of lights is thus a three-dimensional configuration space.
| |||
Left: Cones of light from bulbs suspended above a stage determine circle patterns on the floor. Right: The coordinates for the center and radius for each disc of light indicate whether or not the disc will remain completely within the stage area. |
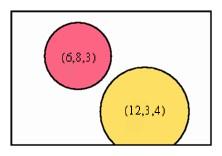
On one level, the use of three coordinates provides a convenient way to record the various lights. For example, the coordinates (6, 8, 3) might indicate a light centered at a stage point 6 feet from the left side and 8 feet from the edge of the stage, having radius 3. On a deeper level, the collections of coordinates define a geometrical space. When mathematicians call a collection a space, that term generally indicates that more structure is present. In the case at hand, it is possible to use the coordinates to determine particular properties of the lights and their relationship to the stage and to one another. For example, the light with coordinates (6, 8, 3) stays on the stage, while the light corresponding to (12, 3, 4) comes off the front of the stage. It is easy to determine a rule that tells when a light stays away from the front rim of the stage, namely that the second coordinate is larger than the third. In this way we see a relationship between the geometry of the configurations and the relationships among their coordinate representations.
The lighting director can also solve more complex problems by referring to the coordinates. For example, when will one spot be contained in another? This happens when the distance between the points in the plane given by the first two coordinates is greater than the difference of the third coordinates. In this space, the three coordinates do not play the same roles, so even though the geometry of the configuration space is three-dimensional, it is not identical with the usual geometry of ordinary three-space.
This example sheds light on the introduction of time as a fourth coordinate. Sooner or later everyone hears a statement like ``Time is the fourth dimension,'' and that idea represents a limitation of the idea of dimensionality. Already in the last century writers realized that in many situations time can be viewed as a fourth dimension, but by no means does it demand any special role as the fourth dimension. When physicists, especially relativity physicists, specify an event by giving three space coordinates and one time coordinate, they are using a four-dimensional configuration space. This space has its own geometry, but it is not the same as the geometry of the four-dimensional space that extends ordinary plane and solid geometry, where distance is given by the generalized Pythagorean theorem. In relativity, the distance between two events is given by [(x-x')2 + (y-y')2 + (z-z')2 - (t-t')2]1/2 so the time coordinate, measured in special units related to the speed of light, appears in the expression with a negative sign, not a positive sign as in the generalized Pythagorean theorem.
| ||
A simple molecule is modeled by a collection of nonoverlapping spheres joined by rods. |
The three-dimensional configuration space of spotlights is analogous to a four-dimensional geometry occurring in molecular modeling. The atoms making up a molecule are modeled by small spheres of varying radii. The description of the arrangement of atoms in a particular molecule consists of a list of such spheres, each with three coordinates to specify its center and one coordinate to give the radius. Thus the configuration space of atoms is four-dimensional. We can describe such a molecule to a graphics computer and ask it to display any particular view of the object. The computer can determine that two atoms do not intersect by checking an algebraic condition in four coordinates, namely (x-x')2 + (y-y')2 + (z-z')2 - (r+r')2 < 0. The geometry of this configuration space is much closer to that of relativity theory than it is to ordinary Euclidean four-dimensional geometry.
The lighting system that began our discussion can be even more complicated if each of the lights also possesses a rheostat to control the current, and hence the brightness of the spot. Adding the coordinate for brightness causes the configuration space to become four-dimensional. If we want to indicate the color of each spotlight as well, then the dimensionality jumps again. Usually we describe a color using separate numbers for hue, saturation, and value, or using three numbers giving the relative amounts of red, yellow, and blue (for pigments) or red, green, and blue (for lights). In any case the specification of color requires three more coordinates, so the lighting director will have seven coordinates for each spotlight--two for floor position, one for radius, one for brightness, and three for color. Thus it is that a simple example leads to a configuration space of high dimensionality.
The universe of modern physics is much more complicated than Einstein's description of events based on three dimensions of space and one of time. Some current models keep track of ten dimensions that act like space and one that acts like time to give an 11-dimensional configuration space. Another important model uses a configuration space with 26 dimensions. In each case the choice of the model depends to some degree on the kinds of mathematics that apply in these dimensions, as an aid for keeping track of the complex interrelationships among events in these higher-dimensional spaces.
| Configuration Spaces of
Segments and Lines | ||
| Table of Contents | ||
| Anthropological Sites and the
Space of Circles |