 |
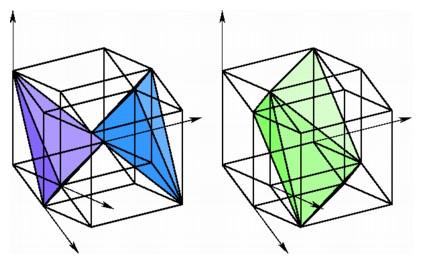
Hyperplane slices of the hypercube containing vertices with coordinates adding to 1 or 3 are tetrahedra (left), while the slice having vertices with coordinates adding to 2 is an octahedron (right).
When we analyzed objects in three- and four-space from a synthetic viewpoint, we learned quite a bit about the structure of cubes and hypercubes by keeping track of a sequence of slices perpendicular to the longest diagonal. The coordinate approach gives us a fresh look at this procedure. Some of the important geometric relationships among the slices already appear in the patterns of the coordinates.
As we slice a unit cube by planes perpendicular to the long diagonal, the first slice we get is the single vertex (0, 0, 0). Then comes the equilateral triangle with vertices (1, 0, 0), (0, 1, 0), and (0, 0, 1), having coordinates adding up to 1. As the slicing plane moves farther from the origin, the next vertices we encounter are those having coordinates adding up to 2 -- (0, 1, 1), (1, 0, 1), and (1, 1, 0) -- also forming the vertices of an equilateral triangle. The final vertex that we hit is (1, 1, 1), the unique vertex of the cube having coordinates adding up to 3.
We may carry out the same analysis for the hypercube in four-space. As we slice the hypercube perpendicular to the long diagonal from (0, 0, 0, 0) to (1, 1, 1, 1), the first slice is again the origin, (0, 0, 0, 0). Next comes the three-simplex with vertices (1, 0, 0, 0), (0, 1, 0, 0), (0, 0, 1, 0), and (0, 0, 0, 1), having coordinates adding up to 1. In general, the vertices lying in a particular hyperplane perpendicular to this long diagonal will have coordinates adding up to a given number from 0 through 4. The unique vertex with coordinates adding to 0 is the origin, and the opposite vertex (1, 1, 1, 1) is the unique vertex of the hypercube having coordinates adding up to 4. The slice containing vertices with coordinates adding up to 3 will be a three-simplex, having vertices (0, 1, 1, 1), (1, 0, 1, 1), (1, 1, 0, 1), and (1, 1, 1, 0). Exactly in the middle we find a very interesting slice, where the coordinates add up to 2. There are six vertices in this slice -- (1, 1, 0, 0), (1, 0, 1, 0), (1, 0, 0, 1), (0, 1, 1, 0), and (0, 0, 1, 1) -- and these form the vertices of a regular octahedron halfway through the hypercube.
| ||
Hyperplane slices of the hypercube containing vertices with coordinates adding to 1 or 3 are tetrahedra (left), while the slice having vertices with coordinates adding to 2 is an octahedron (right). |
Note that we find six vertices in the middle level of the hypercube since there are six ways to choose two zeros and two ones for the four coordinates. By studying the combinations of zeros and ones, we can predict the number of vertices in each slice. For the n-cube with vertices having coordinates 0 or 1, the slice perpendicular to the longest diagonal will start with the vertex having all coordinates 0 and end with the vertex having all coordinates 1. The slice containing vertices having coordinates adding up to k will contains C(n, k) vertices, the number of ways to choose k coordinates equal to 1 and the rest 0. As the observation suggests, the numbers of vertices in hyperplane slices appear as the numbers in the rows of Pascal's triangle.
| Coordinates for Regular Polyhedra | ||
| Table of Contents | ||
| Coordinates for the n-Simplex |