 |
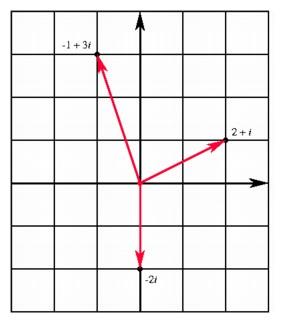
Complex numbers in the coordinate plane.
Up to this point, we have considered pairs, triples, and n-tuples of real numbers, starting with the points on a one-dimensional real number line. Although the real numbers are sufficient for very many purposes in algebra and geometry, they are inadequate for solving some simple equations. For example, since the square of any real number is never negative, it is impossible to find a real number that solves the equation x2 = -1. To construct a larger number system where this equation can be solved, mathematicians introduced a new symbol, i, with the property that i2 = -1. In order still to be able to add numbers and multiply them by real numbers, they had to include in their system all numbers of the form x + yi, with x and y real. They called this collection the complex numbers.
| ||
Complex numbers in the coordinate plane. |
Each complex number x + yi corresponds to a number pair (x, y) in the plane, so we may say that the complex numbers form a two-dimensional collection. The two coordinates of the pair (x, y) are called the real part and the imaginary part of the complex number. We already know how to add number pairs and multiply them by real scalars, and this leads to rules for addition and scalar multiplication for complex numbers. The sum of x + yi and u + vi is (x + u) + (u + v)i, and the product of x + yi by the real number c is cx + (cy)i.
But it is also possible to define a multiplication of one complex number with another, giving as the product of two complex numbers
| ||
The graph of the real parabola in real two-space. |
One of the most effective techniques in ordinary analytic geometry is the graphing of functions of one real variable on a two-dimensional grid. In ordinary analytic geometry, the equation u = x2 can be graphed in the plane by plotting all pairs of the form (x, x2). The geometric form of this graph is a parabola, symmetric with respect to the vertical axis and passing through the origin. This representation gives a tremendous amount of insight into the symmetry of the function as well as the location of its minimum points.
What about complex functions of a complex number? We can still talk about the equation w = z2, where now z and w represent complex numbers. We can analyze the function algebraically all right, but how can we graph it? A problem with dimensions precludes a simple graph on paper. A single complex number already requires two real numbers, its real and imaginary parts, so we have two real coordinates for z and two more for w. The total graph requires four real dimensions, two for the domain and two for the range, giving a two-dimensional surface in four-dimensional space. To study such an object from a geometric point of view, we can try all of the techniques we have used in investigating hypercubes and other figures in four-dimensional space.
Already in the last century, mathematicians created plaster models to show projections of such complex function graphs into three-space, but it was often difficult to imagine how these various views could all arise from the same object in four-space. The fulfillment of this approach only came much later, in our own time, with the development of interactive computer graphics. Many modern graphics computers can rotate filled-in surfaces in four-dimensional space almost as fast as in three-space, so we can see what happens to the images of the graph of a complex function as we rotate it in four-space and project it into our ordinary viewing space.
A basic example demonstrates how the computer handles the equations of complex functions. We have already discussed the parabola in the plane, which is the graph of the real squaring function u = x2. For complex numbers, the relation w = z2, where z = x + yi and w = u + vi, can be expressed in terms of the real coordinates x, y, u, and v. The usual rules of algebra give
Therefore u = x2 - y2 and v = 2xy. The analogue in four-space of the graph of the parabola in the plane is the collection of points of the form (z, z2), but now each of these coordinates is determined by two real numbers, for a total of four real coordinates. We may list the two real and imaginary parts of z and the two real and imaginary parts of z2 in a four-tuple (x, y, x2 - y2, 2xy), and the collection of these four-tuples in four-dimensional space will be the graph of the complex squaring function.
Given any point in the (x, y)-plane, we may determine the other two coordinates and plot the points. As usual, one of the most effective ways of visualizing a collection of points in four-space is to project them into the plane or into three-space. The same instructions that enable us to create motion pictures of a rotating hypercube make it possible to project the graph of the complex squaring function from four-space. Projecting into the three-space of the first three coordinates yields (x, y, x2 - y2), the graph of a real function of two variables, a hyperbolic paraboloid. Projecting into the hyperplane determined by the first, second, and fourth coordinates yields (x, y, 2xy), a rotated hyperbolic paraboloid.
More interesting images appear when we project into the hyperplane of the last three coordinates. We obtain the graph of (y, x2 - y2, 2xy), known as the imaginary part of the square root relation. The image is very different from the hyperbolic paraboloids, possessing a singular point at the origin. The figure intersects itself along a ray of double points on a coordinate axis, ending in a so-called "pinch point" at the origin. This example provides one of the most difficult rendering challenges for a graphics computer and yields some of the most interesting images from the space of four dimensions.
| Four-Dimensional Numbers: The Quaternions | ||
| Table of Contents | ||
| Coordinates for Regular Polytopes |