 |
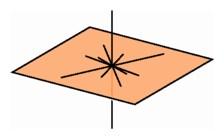
There are many perpendicular lines through a point on a line in space, and these lines fill out the plane perpendicular to the given line through the point.
The ideas of non-Euclidean geometry became current at about the same time that people realized there could be geometries of higher dimensions. Some observers lumped these two notions together and assumed that any geometry of dimension higher than three had to be non-Euclidean. But soon mathematicians realized that there was an essential difference between the two notions. It was perfectly possible to have a higher-dimensional geometry satisfying axioms that were exactly analogous to all the axioms of Euclid, so that any triangle would have its angle sum precisely equal to 180 degrees.
Hermann Grassmann in Germany was one of the first to develop a full geometry that worked in dimensions higher than three, and this notion was extended in England by Arthur Cayley and John J. Sylvester among others. In particular they described a geometry of four dimensions where the fundamental objects were points, lines determined by pairs of points, planes determined by noncollinear triples of points, and hyperplanes determined by noncoplanar quadruples of points. They were able to move into a higher dimension because they added another axiom: outside any given three-dimensional hyperplane, there were other points.
In solid geometry, the analogue of the parallel axiom says that through any point not on a plane, there passes exactly one plane that does not meet the first plane. In four-dimensional geometry, the analogous axiom states that through any point not lying on a hyperplane, there passes exactly one hyperplane not meeting the first hyperplane.
| ||
There are many perpendicular lines through a point on a line in space, and these lines fill out the plane perpendicular to the given line through the point. |
In plane geometry, through a given point on a line there is a unique perpendicular line. In solid geometry, through a given point on a line there are many lines that meet it at a right angle, and these lines all lie on a plane perpendicular to the given line through the point. In four-dimensional geometry, the lines that meet a given line at a given point at a right angle fill out an entire hyperplane.
In solid geometry, through a point on a plane there passes exactly one line perpendicular to the plane. In four-dimensional geometry, through a point on a plane there are manv lines that meet the plane at a right angle, and these lines fit together to form a plane perpendicular to the first plane and meeting the plane at a single point.
It is quite surprising that in four-space two totally perpendicular planes can meet at a point (see diagram on page 148). This concept is so difficult precisely because it is so hard to visualize. But in fact it is not that easy to see that a line in three-space is perpendicular to a plane. If the plane is opaque, then the line appears to come down to the plane and disappear beneath it. If the plane is semitransparent, we might notice that the line, changes color as it goes through. We could move the configuration around to determine if the line is really perpendicular. If we draw a square on the plane and hold the plane so that the square appears as a square, with four equal sides and four right angles, then the perpendicular line will appear as a point. We can do the same in four dimensions with the help of a graphics computer. We can move a configuration of two perpendicular planes around in four-space so that the image on the screen is just a plane, with the other plane being mapped to a point. A good place to find a treatment of results in synthetic geometry of four dimensions is iii the book Geometry of Four Dimensions by Henry Parker Manning.
Eventually the fundamental ideas of Gauss and the development of higher-dimensional analytic geometry led to a beautiful general theory in the dissertation of Bernhard Riemann, who conceived the notion of an n-dimensional manifold with a metric, a rule for assigning lengths to paths. The far-reaching effects of this generalization have changed the way mathematicians view the nature of space, and they formed the necessary background for the appearance of relativity physics. Higher-dimensional analytic methods led some mathematicians to adopt a purely formal approach to geometry, independent of the traditional ways of visualizing geometric objects. But from another point of view, these methods laid the groundwork for the use of computer graphics in investigating objects in higher-dimensional space.
| Immanuel Kant and Nonorientability | ||
| Table of Contents | ||
| Three-Dimensional Non-Euclidean Geometry |