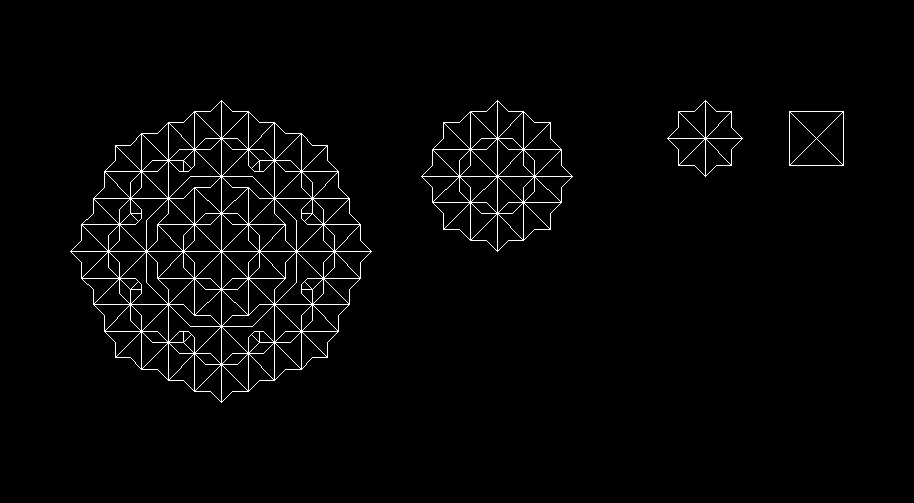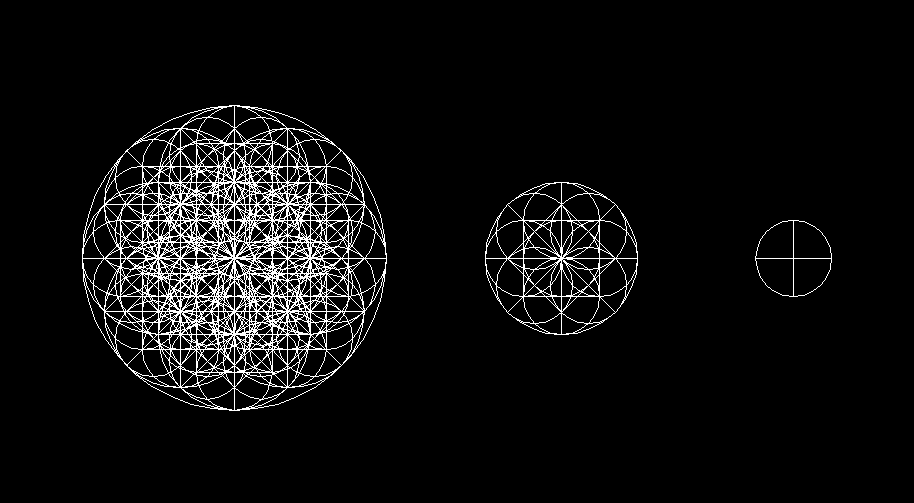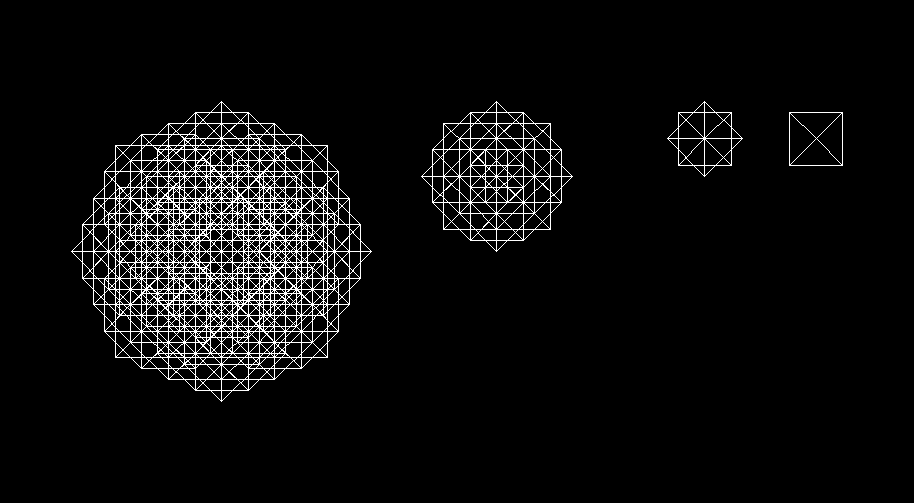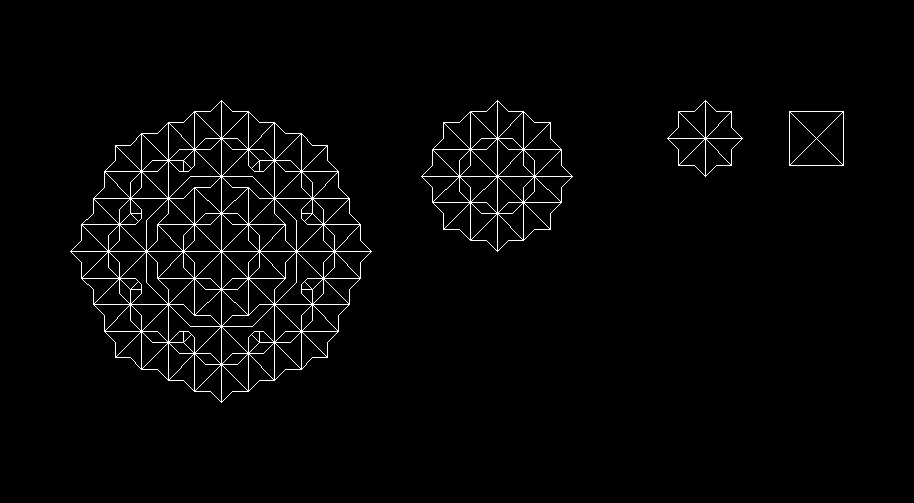Illustrations of Translation
and Rotation
graphics by Samuel
P. Batchelor
Rotating simple shapes can produce very
interesting complex shapes. Here, we start with a circle. If we translate
a copy of this circle so that it is tangent to the original circle's center,
then rotate it about that center 8 times, we get the image below. The process
can be repeated as many times as we like to create more and more complicated
shapes.
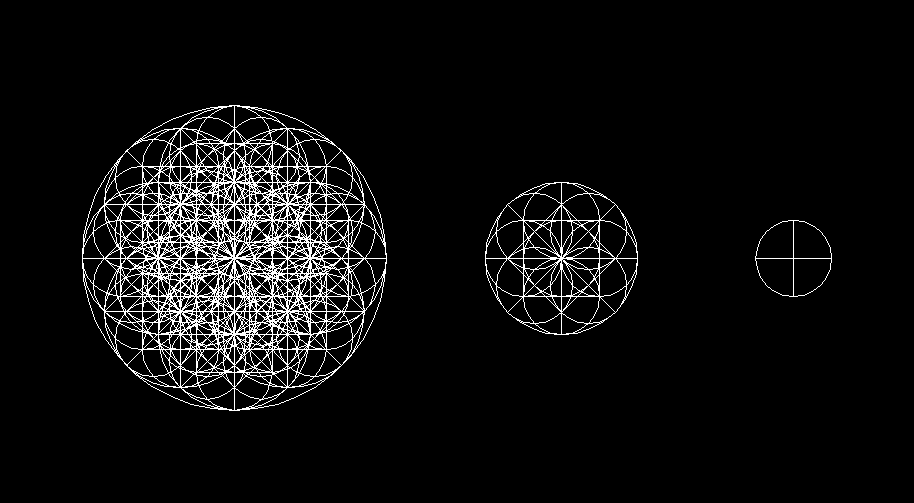
The same process can be used for a square
with an inscribed "x". If we first rotate the square 45 degrees on its
center and then perform the afore-mentioned process (translate the shape
to a position tangent to the side, and rotate 8 times), the image is more
complicated and therefore more interesting.
As we have so often seen in our experiences
with geometry, simple movements can make unexpected larger shapes out of
ordinary ones. If we treat the shape on the far right not as a flat square,
but as a regular pyramid wire model. We turn it into a three-dimensional
design. Viewed from above, it looks exactly the same as before. However,
viewed from an angle it looks like the picture below.

If we fill in the sides of the pyramids
so that they are solid, not wire frame, models, the shape becomes easier
to read.

The solid walls change the aerial view
a little. The walls obscure some of the lines that were previously
visible are now hidden. The new design looks like this: