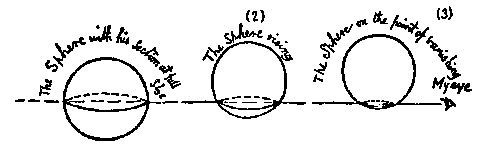Madeline L'Engle's exposition of the concept of multiple dimensions is in Chapter Five: "The Tesseract," of A Wrinkle in Time. Below, a dissection and analysis of her treatment of the concept from a modern and more strictly mathematical point of view… (Italicized passages are from the text and in context as much as possible)Chapter 5:The Tesseract"Yes," Mrs. Which said. "Hhee iss beehindd thee ddarrkness, sso thatt eevenn wee cannott seee hhimm."
L'Engle's treatment of "the darkness" curiously recalls the astronomical concept of dark matter. "The Black Thing" is not necessarily an entity in and of itself; it is observed mainly through its effect on worlds, planets, and galaxies discussed in the book. This is analogous to the modern idea of dark matter in the universe-basically invisible, astronomers note its presence through the gravitational effects of its mass on objects.
Although most of the modern theory of dark matter had been developed since A Wrinkle in Time was published in 1962, the idea of an invisible substance that drastically affects the order and motion of objects is centuries old:
"James Clerk Maxwell (1831-1879), founder of the modern theory of electromagnetism, wrote [that] 'Whatever difficulties we may have in forming a consistent idea of the constitution of the aether [proposed invisible 'glue' of the universe, which some mathematicians have purported to exist between objects in space, both on large and small scales], there can be no doubt that the interplanetary and interstellar spaces are not empty, but are occupied by a material substance or body, which is certainly the largest, and probably the most uniform body of which we have any knowledge.'"
(Quoted by Rudy Rucker in his book The Fourth Dimension. Boston: Houghton Mifflin Company. 1984. Page 71.)
Meg began to cry, to sob aloud. Through her tears she could see Charles Wallace standing there, very small, very white. Calvin put his arms around her, but she shuddered and broke away, sobbing wildly. Then she was enfolded in the great wings of Mrs. Whatsit and she felt comfort and strength pouring through her. Mrs. Whatsit was not speaking aloud, and yet through the wings Meg understood words.
"My child, do not despair. Do you think we would have brought you here if there were no hope? We are asking you to do adifficult thing, but we are confident that you can do it. Your father needs help, he needs courage, and for his children he may beable to do what he cannot do for himself."
"Nnow," Mrs. Which said. "Arre wee rreaddy?"
"Where are we going?" Calvin asked.
Again Meg felt an actual physical tingling of fear as Mrs. Which spoke.
"Wwee musstt ago bbehindd thee sshaddow."
"But we will not do it all at once," Mrs. Whatsit comforted them. "We will do it in short stages." She looked at Meg. "Now wewill tesser, we will wrinkle again. Do you understand?"
"No," Meg said flatly.
Mrs. Whatsit sighed. "Explanations are not easy when they are about things for which your civilization still has no words. Calvintalked about traveling at the speed of light. You understand that, little Meg?"
Incidentally-The speed of light equals 3 x 10^8 meters/second, which is roughly equivalent to 670 million miles per hour. It is believed to be physically impossible for humans to travel at this speed, and at any rate, it would do a number on the body.
"Yes," Meg nodded.
"That, of course, is the impractical, long way around. We have learned to take short cuts wherever possible."
"Sort of like in math?" Meg asked.
"Like in math." Mrs. Whatsit looked over at Mrs. Who.
"Take your skirt and show them."
"La experiencia es la madre de la ciencia. Spanish, my dears. Cervantes. Experience is the mother of knowledge." Mrs. Who took a portion of her white robe in her hands and held it tight.
"You see," Mrs. Whatsit said, "if a very small insect were to move from the section of skirt in Mrs. Who's right hand to that in her left, it would be quite a long walk for him if he had to walk straight across."
Swiftly Mrs. Who brought her hands, still holding the skirt, together.
"Now, you see," Mrs. Whatsit said, "he would be there, without that long trip. That is how we travel."
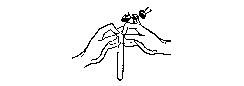
Mrs. Who's movement of her skirt changes the one dimensional line of before. The curve she forms is still technically one dimensional (that is, any point on the curve can be described by a single coordinate), but by connecting the two endpoints of the line together, she describes an elliptical polygon, which exists in a two dimensional plane. Mrs. Who's "trip" had to involve the next higher dimension. The "wrinkle in time" concept hinges upon using the fourth (or fifth-more on this later) dimension to similarly bend and join parts of the familiar three (or four) dimensional world in which the reader, L'Engle, and our characters live. The idea is that the fabric of space/time 'wrinkles'-folds onto itself, creating new paths for travel.
By creating the ellipse with the line of Mrs. Who's skirt, L'Engle's utilizes the idea of two points' possibly being the same point in the next higher dimension. An infinite series of (x,y) coordinates in a Cartesian plane could have the same z coordinate in the third dimension-thus, in the next higher dimension, these two points are in the same "place." It is possibly to algebraically extrapolate this idea into the third and fourth dimension. An infinite series of (x, y, z) coordinates in three dimensional space could all have the same coordinate q in the fourth dimension. This entire series of points could all exist in the same "place" in the fourth dimension, thus making travel from three dimensional point to three dimensional point both possible and instantaneous in the fourth dimension.
Charles Wallace accepted the explanation serenely. Even Calvin did not seem perturbed. "Oh, dear," Meg sighed. "I guess I am a moron. I just don't get it."
A large part of the lasting appeal of "A Wrinkle in Time" is the fact that the hero is quite obviously flawed and easy to relate to. An interesting parallel exists here between Meg's understanding of math and the mathematical concepts used in the book. Meg relies on shortcuts and a sort of intuition to handle her math work in school. She does not do mathematics in traditional ways. The entire area of dimensions and theoretical geometry has, by necessity, been trailblazed by those mathematicians who used traditional mathematics in non-traditional ways. These concepts have also been investigated by 'amateur' mathematicians-writers such as Jorge Luis Borgesand Gabriel Garcia Marquez have used dimensional and time-related concepts in their works. Many children's authors have investigated new ways of travel that imply, if not other dimensions, different modes of looking at our reality. Lewis Carrol sends Alice to another world through the looking glass and down rabbit holes, and C.S. Lewis uses a wardrobe. Edwin Abbott Abbott, one of the first people to think seriously about dimensions and their implications, wrote a book called Flatland in 1884 about shapes that travel from dimension to dimension.
"That is because you think of space only in three dimensions," Mrs. Whatsit told her. "We travel in the fifth dimension. This issomething you can understand, Meg. Don't be afraid to try. Was your mother able to explain a tesseract to you?"
This is where L'Engle's math gets a little confusing. Traditionally, the tesseract is a term used to describe the hypercube. The hypercube is an object in the fourth dimension, analogous to a point in the zero dimension, a line in the first dimension, a square polygon in the second dimension, and a cube in the third dimension. Thus, a "tesseract" is an object of the fourth dimension, not the fifth.
"Well, she never did," Meg said. "She got so upset about it. Why, Mrs. Whatsit? She said it had something to do with her and Father."
"It was a concept they were playing with," Mrs. Whatsit said, "going beyond the fourth dimension to the fifth. Did your mother explain it to you, Charles?"
It's interesting that L'Engle assumes here that everyone is comfortable with the fourth dimension's existence at all. Having taken an informal poll on the campus of Yale University, I have found that a surprisingly vocal minority of students (close to a majority) don't believe that a fourth dimension (let alone the fourth dimension) exists. (Incidentally, according to The American Heritage Dictionary, there's no such thing as a tesseract. Maybe Mr. Jenkins wrote it.) Many of those students who did believe that it exists are even more vague about it than L'Engle, when she refers to it simply as time. More on this later.
"Well, yes." Charles looked a little embarrassed. "Please don't be hurt, Meg. I just kept at her while you were at school till I got it out of her."
Meg sighed. "Just explain it to me."
"Okay," Charles said. "What is the first dimension?"
Note: The "zero" dimension is a single point
"Well--a line: ----------------"
"Okay. And the second dimension?"
"Well, you'd square the line. A flat square would be in the second dimension."
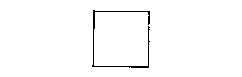
L'Engle's use of the verb "to square" is a little curious. The American Heritage (1983) Dictionary's definition of "square" as a verb is "to multiply (a number, quantity, or expression) by itself." If we work with a single variable, x, then the zero dimension (i.e. x^0) equals one and is a single point. The first dimension would be x^1, or x. If we find the second dimension by squaring the first, then we'd get x times x, or x^2. So far so good, but later…
"And the third?"
"Well, you'd square the second dimension. Then the square wouldn't be flat any more. It would have a bottom, and sides, and a top."
If we were to follow the pattern above, then we'd square the second dimension, or x^2. However, (x^2)^2 is x^4, not x^3. (This follows from the additive property of multiplying exponents) To go from one dimension (expressed in terms of x), you only need to multiply the previous dimension by x. This is not a drastic mistake, but it shows that the mathematics in A Wrinkle in Time were not L'Engle's primary concern. In many ways, the mathematical concepts in A Wrinkle in Time were used as a vehicle to provide an opportunity for L'Engle to express her religious beliefs.
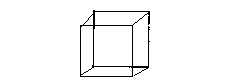
"Well, I guess if you want to put it into mathematical terms you'd square the square. But you can't take a pencil and draw it the way you can the first three. I know it's got something to do with Einstein and time. I guess maybe you could call the fourth dimension Time."
Okay, this paragraph has some serious mathematical inaccuracies. First of all, one can draw a hypercube (or the outline/shadow of one) using a pencil. Of course, this figure isn't perfect. But we can all draw a three-dimensional cube on a blackboard and understand what we're seeing, and this is the same idea. See below.

Secondly, L'Engle calls the fourth dimension the square of a square. In algebraic terms, this would be expressed as (x^2)^2, or x^4, which is accurate. It's curious that L'Engle had this concept right and not the previous. However, she didn't get to the fourth dimension directly via the third dimension, as in (x^3) times x equals x^4. If she had been consistent with this progression in the chapter, the math would have actually been simpler and more accessible for her readers.
Calling the fourth dimension "something to do with Einstein and time" is a gross oversimplification. Algebraically, the fourth dimension is a simple extension of basic mathematical principles in the first, second, and third dimensions.L'Engle actually recalls the aforementioned Flatland by referring to the fourth dimension as time. In Flatland, a creature (called A. Square) lives in a two-dimensional flat world. A. Square is visited by a sphere, from the third dimension. Obviously, all of the sphere cannot exist in Flatland at the same time. The sphere is forced to travel through Flatland one part at a time, as shown below in an original illustration by Abbott Abbott from the book.
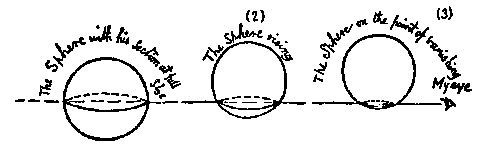
A. Square's view of the sphere is always changing-he first sees a point, then the outline (actually, he sees only part of the curve) of a small circle, then a larger circle, then a larger, and so on until the sphere crosses Flatland at its diameter and is at its largest. Then the circles that A. Square sees get smaller again, until the sphere shrinks back down into a point. A. Square sees the sphere as movement, as constantly changing. In the book, he says that he has seen the "lifetime" of the sphere. A. Square has seen change over time. To A. Square living in the second dimension, an object from the third dimension appears as movement or "time" in his world. This idea is one reason that some people living in the third dimension call the fourth dimension time. If we saw a fourth dimensional object enter our third dimensional space, we'd see it as movement and time.
"That's right," Charles said. "Good girl. Okay, then, for the fifth dimension you'd square the fourth, wouldn't you?"
Well, no. You know by now that if we squared the fourth dimension we wouldn't get the fifth dimension. (x^4)^2 equals x^8, not x^5. To go to the fifth dimension from the fourth, you multiply the fourth dimension by x, as in (x^4) times x equals x^5. Is this getting more familiar now?
"I guess so."
"Well, the fifth dimension's a tesseract. You add that to the other four dimensions and you can travel through space without having to go the long way around. In other words, to put it into Euclid, or old-fashioned plane geometry, a straight line is not the shortest distance between two points."
L'Engle is combining a lot of ideas here-folding dimensions up in the next dimension, "adding" dimensions-that don't completely follow. The idea that "a straight line is not the shortest distance between two points" is interesting, but L'Engle should have added the qualifier "in higher dimensions."
For a brief, illuminating second Meg's face had the listening, probing expression that was so often seen on Charles's. "I see!" she cried. "I got it! For just a moment I got it! I can't possibly explain it now, but there for a second I saw it!"
It's tough to imagine the fourth dimension, since our eyes are conditioned from birth to recognize just the third. Visualization is definitely possible (honestly), and it can occur in this sudden flash that Meg has here.
She turned excitedly to Calvin. "Did you get it?"
He nodded. "Enough. I don't understand it the way Charles Wallace does, but enough to get the idea."
"Sso nnow wee ggo," Mrs. Which said. "Tthere iss nott all thee ttime inn tthe worrlld."
"Could we hold hands?" Meg asked.
Calvin took her hand and held it tightly in his.
"You can try," Mrs. Whatsit said, "though I'm not sure how it will work. You see, though we travel together, we travel alone. We will go first and take you afterward in the backwash. That may be easier for you."
This idea of "backwash" is interesting. Some projections of the hypercube/tesseract into the second dimension show one cube with a smaller cube within it, and the larger cube appears to be spitting out the smaller cube. As it is spit out the smaller cube grows, and the larger cube shrinks, and the larger cube become the smaller cube and the smaller cube becomes the larger cube. It does almost look like the smaller cube is being dragged by the larger, in at of "backwash."
As she spoke the great white body began to waver, the wings to dissolve into mist. Mrs. Who seemed to evaporate until there was nothing but the glasses, and then the glasses, too, disappeared. It reminded Meg of the Cheshire Cat.--I've often seen a face without glasses, she thought;--but glasses without a face! I wonder if I go that way, too. First me and then my glasses?
She looked over at Mrs. Which. Mrs. Which was there and then she wasn't.
There was a gust of wind and a great thrust and a sharp shattering as she was shoved through--what? Then darkness; silence; nothingness. If Calvin was still holding her hand she could not feel it. But this time she was prepared for the sudden and complete dissolution of her body. When she felt the tingling coming back to her fingertips she knew that this journey was almost over and she could feel again the pressure of Calvin's hand about hers.
Without warning, coming as a complete and unexpected shock, she felt a pressure she had never imagined, as though she were being completely flattened out by an enormous steam roller. This was far worse than the nothingness had been; while she was nothing there was no need to breathe, but now her lungs were squeezed together so that although she was dying for want of air there was no way for her lungs to expand and contract, to take in the air that she must have to stay alive. This was completely different from the thinning of atmosphere when they flew up the mountain and she had had to put the flowers to her face tobreathe. She tried to gasp, but a paper doll can't gasp. She thought she was trying to think, but her flattened-out mind was as unable to function as her lungs; her thoughts were squashed along with the rest of her. Her heart tried to beat; it gave a knifelike, sidewise movement, but it could not expand.
It's interesting to try to imagine our third dimensional bodies being suddenly transported to a two dimensional world. For one thing, our lungs couldn't expand; we couldn't breathe. All of our blood vessels would be squished flat-could blood move through veins and arteries like that? Digestion, muscle control, standard movement, standard thinking (with a flat brain?) would all be out of the question.
But then she seemed to hear a voice, or if not a voice, at least words, words flattened out like printed words on paper, "Oh, no! We can't stop here! This is a two-dimensional planet and the children can't manage here!"
She was whizzed into nothingness again, and nothingness was wonderful. She did not mind that she could not feel Calvin's hand, that she could not see or feel or be. The relief from the intolerable pressure was all she needed.
Then the tingling began to come back to her fingers, her toes; she could feel Calvin holding her tightly. Her heart beat regularly; blood coursed through her veins. Whatever had happened, whatever mistake had been made, it was over now. She thought she heard Charles Wallace saying, his words round and full as spoken words ought to be, "Really, Mrs. Which, you might have killed us!"
This time she was pushed out of the frightening fifth dimension with a sudden, immediate jerk.
There is another way to look at the fourth/fifth dimension confusion in this chapter. Meg and Calvin and Charles Wallace and the Mrs. W's do travel in fourth dimensional space, presumably, and this travel does take a small amount of time. In this way, their new fourth dimensional world has a small element, or thickness, of the fifth dimension.
There she was, herself again, standing with Calvin beside her, holding onto her hand for dear life, and Charles Wallace in front of her, looking indignant. Mrs. Whatsit, Mrs. Who, and Mrs. Which were not visible, but she knew that they were there; the fact of their presence was strong about her...
Written by Jessica Weare


© 1998 by Eli Weiss. Last modified: Fri 4 Dec 1998