|
Tangent Lines and Normal Vectors
(Page: 1 | 2
) Text If a function f(x) is differentiable at x0, then f(x) will have a tangent line at (x0) with the equation l(x) = f(x0) + f '(x0)(x - x0).
The normal vector at x0, (-f '(x0), 1), is perpendicular to the tangent line.
Demos
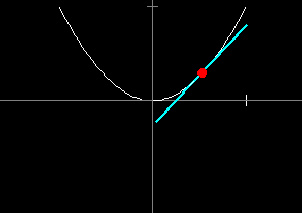
Tangent Lines

| 
|
In this demonstration you can input a function f(x) in the control panel. The graph of f(x) appears in green in a separate window. Next, use the tapedeck in the control panel to choose a point x0 in the domain. The tangent line to the graph at x0 is shown in cyan. 
|
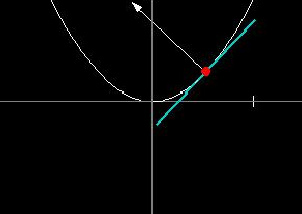
Normal Vectors

| 
|
This demo shows the unit normal vector (in white) to the tangent line for a point x0 in the domain. 
|
Exercises 1. Find equations for the tangent line for each of the following sets of conditions, and check using one of the demos:
- f(x) = x2 at x = 1
- f(x) = sin(x) at x = π
- f(x) = |x| at x = 1
2. Why is the tangent line not defined for f(x) = |x| at x = 0?
3. Describe the tangent lines and normal vectors for any linear function.
4. Note that since the normal vector in this demo always has a vertical component of 1, it can never be parallel to the x-axis. Is this a problem? Why or why not?
|