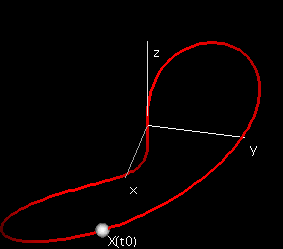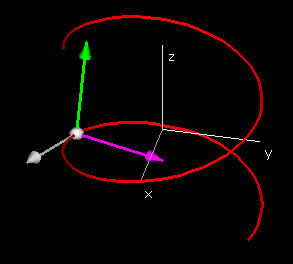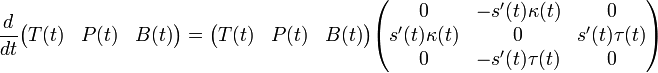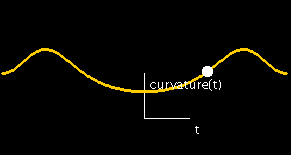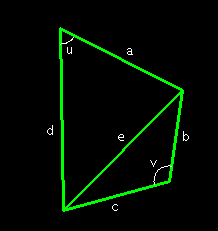
Referring to the above picture, let A be
the area of the figure. Then A=(1/2)adsin(u)+(1/2)bcsin(v).
The law of cosines gives a2+d2-2adcos(u) = e2
= b2+c2-2bccos(v).
Note that a choice of u determines v, so we can call v = v(u). Now we
may consider both of the above equations as depending only on u, and
differentiate both of them with respect to u resulting in
2A'(u) = adcos(u) + bcsin(v(u))v'(u) and 2adsin(u) = 2bcsin(v(u))v'(u).
To maximize A(u) we take 2A'(u) = 0 = adcos(u) + bcsin(v(u))v'(u) ⇒
adcos(u)sin(v(u)) = -bc cos(v(u))sin(v(u))v'(u) = -adsin(u)cos(v(u)), so
cos(u)sin(v(u)) + sin(u)cos(v(u)) = 0 = sin(u + v(u)), so
u+v=π which is the necessary and sufficient condition for the
quadrilateral to be inscribed in a circle.