Desargues' Theorem
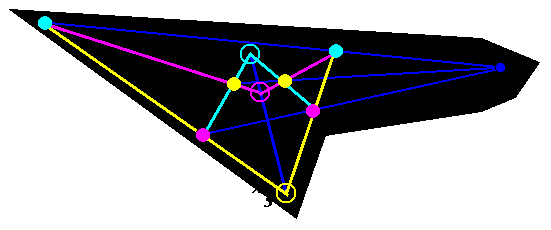
Desargues' Theorem
Refers to the configuration above.
If you start with 6 points--colored cyan,
yellow, and magenta--placed in an arrangement
like the one shown, then the circled intersection
points will lie on a line.
Classical Proof:
Consider a "tripod" T in 3-space formed by 3 coincident lines
and the planes they span. Take two auxilliary planes
and intersect them with T. This intersection will be a
pair of triangles. The intersection points of
corresponding edges of these triangles will lie
on the line of intersection of the auxilliary planes.
Projecting this configuration to the plane gives
Desargues' theorem.
To see this in action, click repeatedly on the
figure below.



