Definitions

 kites 
A  kite  is a convex quadrilateral with an axis
of bilateral symmetry that goes through a pair of
opposite vertices.  (See Figure below.)  Every kite 
is affinely equivalent to a kite K(A) with vertices
(0,1);   (0,-1);  (-1,0);   (A,0)  with A in (0,1).
The kite is called (ir)rational if A is (ir)rational.

Outer billiards is an affinely natural dynamical system, 
so the study of outer billiards on kites reduces to the
study of outer billiards on K(A).

 the outer billiards map 
The  outer billiards map  on K is x0-->x1.
The line segment from x0 to x1 is bisected by a
vertex of K, and a person walking from x0 to x1
sees K on the right.



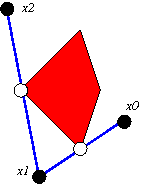Iterating the o.b.m. generates the  forwards orbit 
x0-->x1-->x2-->x3... The backwards orbit
is defined using the inverse o.b.m. Both directions
are defined on a full measure subset of R^2-K.
We call the map o2(x0)=x2 the  square map .

 kinds of orbits 
Reflection in each vertex of K(A) preserves the family
of horizontal lines having height an odd integer.
These are the blue lines in the applet at right.
Hence, any orbit that starts in this set of lines
remains there.  We call such an orbit  special 

We call an outer billiards orbit  erratic 
if both the forwards and backwards orbits are
unbounded, and also enter into every
neighborhood of the vertex set of K. Erratic
orbits oscillate in the widest possible sense.

demo 
The demo at the right lets you see up
to 20 iterates of the o.b.m. on K(3/7).
(We just picked a random example.)

Use the middle mouse button to
select points on the big window.
Use the left/right mouse buttons
to scale the picture. If you don't
have a 3 button mouse, or if yours
is not working properly with the
applet, you can use the mouse 
emulator at the top left.

The applet only lets you plot special
orbits. Use the arrow keys to select
the number of iterates. max=20.
Toggle the two buttons to see
the o.b.m. and/or the square of o.b.m.