Research interests and recent talks and publications
General Research Area: Complex Analysis, Harmonic Analysis and Operator Theory
Brief Research Summary:
My research interests lie in the intersection of Complex Analysis,
Harmonic Analysis and Operator Theory, . Many problems I am
working on have their origin in applications, such as Control Theory
(H-infinity control, etc.), Stationary Random Processes.
My
earlier research deals with Hankel and Toeplitz operators, functional
models of operators, spectral decompositions of operators, spectral
theory of matrix- and operator-valued functions.
Recent
research projects involve classical and non-classical harmonic
analysis, such as: weighted norm inequalities for singular integral
operators, matrix Apweights, wavelet and
frame decompositions, Calderon--Zygmund operators on non-homogeneous
spaces and analytic capacity. Some of the most recent projects in
this directions deal multi-parameter harmonic analysis.
Another
direction of research concerns the Corona Problem and related
topics, in particular the relations between the Corona Problem and
geometry of Hermitian bundles.
The papers below give you general idea of my recent research projects.
Recent papers
All my recent papers are posted on the ArXive, so I am no longer posting the papers on my page.
You can follow this link to get to the ArXive page with my papers
Below are the older, previously posted papers, I am not removing
any links, since not all of them are available in the ArXive. Clicking
on a link brings you either to an ArXive page with the paper or to a
page with short abstract (sometimes there is no abstract) and links to .dvi , .ps and .PDF files with the text.
- Curvature Condition for Noncontractions does not imply Similarity to the Backward Shift, with Hyun Kwon,
arXiv:0903.4423v1 [math.CA]
- Rank one perturbations and singular integral operators, with Constanze Liaw, Journal of Functional Analysis, Volume 257(2009), Issue 6, pp 1947-1975, see also
arXiv:0810.2750v1 [math.FA]
- $H^1$ and dyadic $H^1$, Linear and Complex Analysis: Dedicated to V. P. Havin on the Occasion of His 75th Birthday
(S.
Kislyakov A. Alexandrov, A. Baranov, ed.), Advances in the Mathematical
Sciences, vol. 226, AMS, 2009, pp.~179--194. see also arXiv:0809.3288v1 [math.CA] - Similarity of operators and geometry of eigenvector bundles, with Hyun Kwon, Publicacions Matematiques, 53 (2009), 417-438, see also
arXiv:0712.0114v1 [math.FA]
- A theorem about three quadratic forms, with Oliver Dragičević
and Alexander Volberg, Int. Math. Res. Not. IMRN 2008, Art. ID rnn 072, 9 pp., see also arXiv:0710.3249v1
[math.FA]
- The problem of ideals of
$H^\infty$: beyond the exponent 3/2, Journal
of Functional Analysis, 253 (2007), 220-240, see also
arXiv:math/0702806v1 [math.CV]
- Two weight inequalities for individual Haar multipliers and
other well localized operators, with F. Nazarov,
and A. Volberg, accepted by Math. Research
Letters, see also arXiv:math/0702758v1
[math.CA]
- Carleson Potentials
and the Reproducing Kernel Thesis for Embedding Theorems, with
Stefanie Petermichl and Brett Wick, Illinois Journal of Mathematics, 51 (2007), no. 4, 1249--1263, see also
arXiv:math/0701851v1
[math.CA].
- Estimates in corona theorems for some subalgebras of
$H^{\infty}$,
with A. Sasane, Arkiv för Matematik, v 35, No 2,
351-380, see also arXiv:math/0702754v1
[math.CA]
- Analytic projections, Corona Problem and geometry of holomorphic vector bundles,
with B. Wick,
J. Amer. Math. Soc. 22 (2009), no. 1, 55--76., see also arXiv:math/0702756v1
[math.CA]
- Scalar and vector
Muckenhoupt weights, with M. Lauzon, Indiana Univ. Math. J. 56 (2007), no. 4, 1989--2015..
- Approximation by analytic operator functions. Factorizations and very badly approximable
functions, with V. Peller, Algebra i Analiz 17 (2005), no. 3, 160--183,
see also arXiv:math/0407458v1
[math.FA]
- Very badly approximable
matrix functions,
with V. Peller, Selecta Math. (N.S.), 11 (2005), no. 1,
127--154, see also arXiv:math/0303186v1
[math.FA]
- The Matrix-Valued
Hp Corona Problem in the Disk and Polydisk,
with B. Wick
- An Operator Corona
Theorem
- Lower bounds in the matrix corona theorem and
the codimension one conjecture
- Common Complements of Two Subspaces of a Hilbert Space, with M. Lauzon
- Linear resolvent growth of rank one perturbation of a unitary operator does not imply its similarity to a normal operator, with N. Nikolski
- Bellman function in stochastic control and harmonic analysis, with F. Nazarov and A. Volberg
- Estimates in the Corona Theorem and ideals of
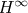 ; a problem of T. Wolff
; a problem of T. Wolff
- Tb Theorem on non-homogeneous spaces,
with F. Nazarov and A. Volberg
- Linear resolvent growth of a weak contraction does not imply its
similarity to a normal operator (with S. Kupin)
- The gap between complex structured singular value
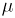 and its upper bound is infinite
and its upper bound is infinite
- Weak type estimates and Cotlar inequalities for Calderon–Zygmund operators on nonhomogeneous spaces
with F. Nazarov and A. Volberg
- Cauchy Integral and Calderon-Zygmund operators on nonhomogeneous
spaces
with F. Nazarov and A. Volberg
- Completely regular multivariate stationary processes and the Muckenhoupt
condition
with A. Volberg
- Weak type estimates and Cotlar inequalities for Calderon-Zygmund
operators on nonhomogeneous spaces
with F. Nazarov and A. Volberg
- Unconditional bases of invariant subspaces of a contraction with
finite defects
- A conterexample to infinitedimensional Carleson imbedding theorem
with F. Nazarov and A. Volberg
- The hunt for a Bellman function: applications to estimates of
singular integral operators
and to other classical problems in harmonic analysis
with F. Nazarov
- The weighted norm inequalities for Hilbert transform are now trivial
with F. Nazarov
- Hilbert transform, Toeplitz operators and Hankel operators, and
invariant
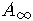 weights ,
weights ,
with A. Volberg and D. Zheng
- Continuous frame decomposition and a vector Hunt -- Muckenhoupt
-- Wheeden Theorem
with A. Volberg
- Wavelets and the angle between past and future
With A. Volberg
- A simple proof of the Hunt -- Muckenhoupt -- Wheeden Theorem
With A. Volberg
- Approximation by analytic matrix functions. The four block problem
With V. V. Peller