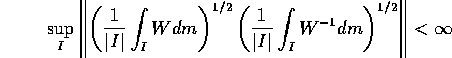
S. Treil and A. Volberg
In the paper we give an alternative proof of the fact that the vector Muckenhoupt condition,
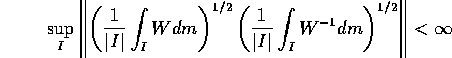
is necessary and sufficient for the boundedness of Hilbert Transform
in
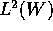with matrix weight (for the
original proof see our paper Wavelets
and the angle between past and future ).
The main technical tool we are using here is a matrix version of the
Littlewood--Paley type inequality that gives an equivalent norm in
the weighte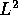d 
space in terms of
weighted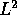 
norm of the
derivative of the harmonic extension see Theorem 4.2 in the paper.
The scalar version was developed by us earlier in the paper
A simple proof of the Hunt -
Muckenhoupt - Wheeden theorem.
This equivalent norm inequality can be viewed as a continuous
analogue of the wavelet type decomposition (Haar system is a Riesz
basis i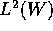n 
) that was used by us in
Wavelets and the angle between past
and future . But in this
case the continuous ``system of coefficients'' (derivatives of
harmonic extension) is over-determined, so it is more appropriate to
call it continuous frame decomposition.
Although the main result about boundedness of the Riesz Projection is already known, we feel that the technique we use is of independent interest, and deserves separate consideration. In a sense the main result is Theorem 4.2 in the text about continuous frame decomposition, and boundedness of the Riesz Projection serves as an illustration of usefulness of this theorem.